안녕하세요😎 백엔드 개발자 제임스입니다 :)
오늘 포스팅은 백준의 2156번 포도주 시식 문제를 정리하려고 합니다. 이 문제는 동적 계획법에 해당하는 문제로, 동적 계획법 풀이 전략을 이해하고 있으면 어렵지 않게 풀 수 있습니다. 반대로 말하면, 동적 계획법의 개념을 제대로 알 수 있는 문제라 할 수 있겠습니다. 저 또한 해당 문제를 풀면서 동적 계획법에 대해서 다시 이해할 수 있게 되었습니다.
문제의 자세한 내용은 아래 링크를 참고해주세요.
https://www.acmicpc.net/problem/2156
2156번: 포도주 시식
효주는 포도주 시식회에 갔다. 그 곳에 갔더니, 테이블 위에 다양한 포도주가 들어있는 포도주 잔이 일렬로 놓여 있었다. 효주는 포도주 시식을 하려고 하는데, 여기에는 다음과 같은 두 가지 규
www.acmicpc.net
Problem
테이블 위에 포도주가 들어있는 잔이 일려로 있습니다. 각각에는 서로 다른 양이 들어있습니다. 이 때 어떤 포도주 잔을 선택했을 때 최대의 양을 마실 수 있는지 찾는 문제입니다. 단 두 가지에 조건이 있습니다.
1. 포도주 잔을 선택하면 그 잔에 들어있는 포도주는 모두 마셔야 하고, 마신 후에는 원래 위치에 다시 놓아야 한다.
2. 3잔을 연속으로 마실 수 없다.
ex) 각각 양이 6, 10, 13, 9, 8, 1 이 들어있는 잔이 6개 있을 때, [첫 번째, 두 번째, 네 번째, 다섯 번째] 잔을 선택하면 총 포도주 양이 33으로 최대로 마실 수 있습니다.

풀이 아이디어
설명에 앞서, 각각 [6, 10, 13, 9, 8, 1] 의 양을 갖고 있는 포도주잔 6개가 있다고 가정하겠습니다.

우리는 동적 계획법(Dynamic Programming) 전략을 활용해서 해당 문제를 해결하려고 합니다. 여기서 동적 계획법 전략은 어떠한 기준으로 문제를 최하위까지 나누고, 가장 작은 문제에서 얻은 해답을 활용하면서 본래의 (최상) 문제를 해결하는 방식입니다.
그렇다면 문제는 어떻게 쪼갤 수 있을까요? 주로 문제를 나누는 기준은 선택한 요소가 포함되었을 때와 포함되지 않았을 때로 나눕니다. 트리 형태로 그림을 그리면서 자세하게 설명하도록 하겠습니다.
(1) 첫 번째 포도주잔 선택하여, 포함했을 때와 포함하지 않았을 때

가장 먼저 DP(0)은 아무 포도잔도 선택하지 않았을 때입니다. 여기서 DP()는 포도잔의 총 양을 저장해둔 공간이라고 생각하면 좋을 것 같습니다. 이어서 포도잔 한 개를 포함했을 때와 포함하지 않았을 때로 나누었는데요. 나뉘어진 두 결과에서 최댓값은 6이기 때문에 DP(1)에는 6이 저장됩니다.
(2) 두 번째 포도주잔을 선택하여, 포함했을 때와 포함하지 않았을 때

다음은 두 번째 포도잔을 포함했을 때와 포함하지 않았을 때입니다. 당연히 두 잔을 모두 포함했을 때가 최댓값이기 때문에 따로 비교할 필요없이 DP(2)에는 6+10인 16이 저장됩니다.
(3) 세 번째 포도주잔을 선택하여, 포함했을 때와 포함하지 않았을 때

세 번째 포도잔까지 포함했을 때와 포함하지 않았을 때입니다. 이제부터 다소 복잡할 수 있습니다. 먼저 조건에 따랐을 때, 연속 세잔은 선택할 수 없기 때문에 세 잔 모두 포함된 경우는 케이스에서 제외시킵니다. 그리고 세 잔 중 두 잔을 선택했을 때가 한잔만 선택할 때보다 당연하게 높은 양을 갖기 때문에 한잔만 있는 경우도 케이스에서 제외시킵니다.

즉, 위 그림에서 처럼 세 개의 케이스가 있는 것입니다.
(4) 네 번째 포도주잔을 선택하여, 포함했을 때와 포함하지 않았을 때
빠른 전개를 위해 불필요한 케이스는 생략했습니다.
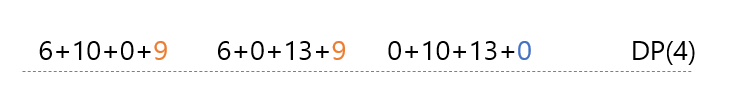
이번은 네 번째 포도주 잔을 선택하여 포함할 때와 포함하지 않을 때 나올 수 있는 케이스입니다. 여기서 나오는 최대값이 DP(4)에 저장되는 것인데요. (1) 먼저 네 번째 잔을 포함할 경우, 두 번째 잔 또는 세 번째잔을 제외시켜야 합니다. (2) 네 번째 잔을 포함하지 않아도 포도주의 양은 최대값을 가질 수 있습니다. 따라서 포함하지 않은 경우도 고려해야 합니다. 이때는 조건을 따르기 위해 첫번째 잔을 제외시킵니다. 아래에서 조금 더 이해하기 쉽게 설명하도록 하겠습니다.
포도주 잔을 3개 이상 선택할 때부터는 (연속 3개 선택 불가) 조건을 신경써야 합니다. 다시 말해서, 마지막 잔을 포함시킬 때 앞에 두 잔이 어떻게 선택되었는지 체크해야 하는 것이죠.

만약 마지막 잔이 포함 될 경우에는 앞에 두 잔을 전부 포함시킬 수 없습니다. 대신 두 잔보다 앞에 있는 잔은 선택할 수 있게 됩니다. 가령 9를 포함시켰을 때 6처럼 입니다. 반면 마지막 잔이 포함되 지않을 경우에는 앞에 두 잔을 선택할 수 있습니다. 그렇다면 당연하게도 두 잔보다 앞에있는 잔은 포함시킬 수 없게 됩니다. 여기서 포인트는 마지막 잔에서 세 잔 앞에 위치한 잔들의 최대값은 이미 저장해 두었던 정보를 활용합니다.
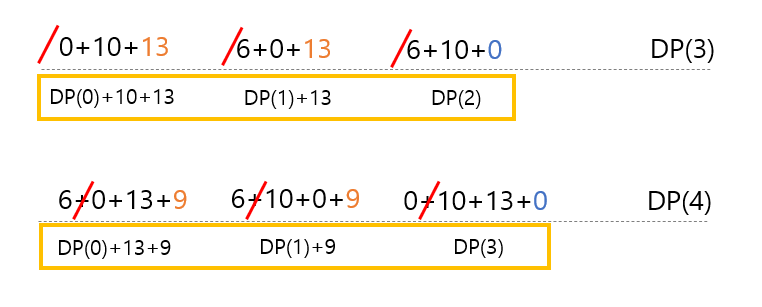
위 그림이 앞에서 저장했던 정보를 활용한 점화식입니다. 마지막 잔을 포함하지 않을 경우에는 어차피 아무 영향이 없기 때문에, 이전에 저장해뒀던 최대값이 해당 부분의 값이 됩니다.
점화식 일반화
이번에는 포도주의 잔이 N개일 경우의 점화식을 일반화해보겠습니다. 현재 위치를 i 라고 했을 때, Wine() 은 해당 위치의 포도주 양이고 DP()는 저장된 포도주 양입니다.
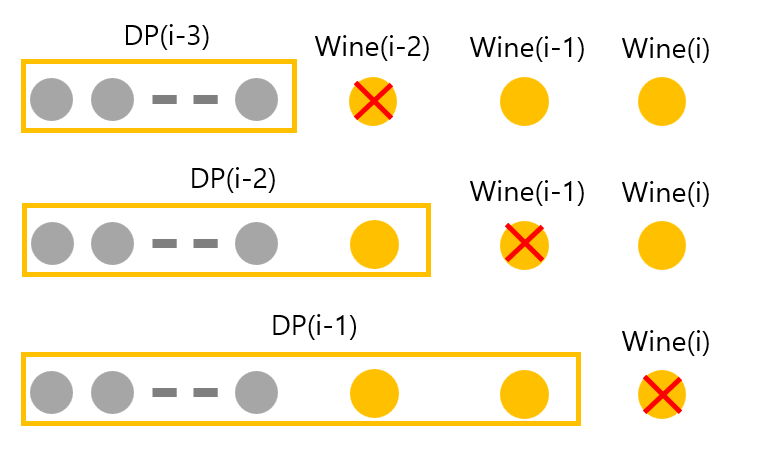
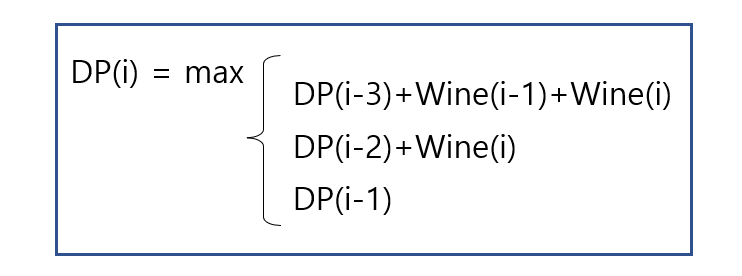
이제 이를 토대로 코드를 작성하도록 하겠습니다.
코드 작성
포도주 2잔 이하일 때는 별다른 고려없이 포함시키면 되기 때문에, DP 배열에 미리 저장합니다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import static java.lang.Math.max;
public class Main {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
public static void main(String[] args) throws IOException {
int N = Integer.parseInt(br.readLine());
// 저장위치의 혼란이 오지 않도록, 인덱스 0번을 더미데이터로 활용
int[] wine = new int[N+1];
int[] dp = new int[N+1];
for (int i = 1; i <= N; i++) {
wine[i] = Integer.parseInt(br.readLine());
}
dp[1] = wine[1]; // 포도주가 한 잔 있을 때
// 런타임 에러 방지
if (N >= 2) {
dp[2] = dp[1] + wine[2]; // 포도주가 두 잔 있을 때
}
for (int i = 3; i <= N; i++) {
dp[i] = max(
dp[i - 1], max(dp[i - 2] + wine[i], dp[i - 3] + wine[i - 1] + wine[i]));
}
System.out.println(dp[N]);
}
}코드를 보다시피 동적 계획법은 점화식을 잘 정리하고, 그대로 코드로 작성하면 무리없이 문제를 해결할 수 있습니다.
여기서 주의해야할 점은 먼저 저장된 위치와 인덱스를 잘 생각해야합니다. 헷갈리지 않기 위해서 좋은 방법은 더미 데이터를 만드는 것이겠죠? 또 런타임 에러(ArrayIndexOutOfBounds)를 조심해야 합니다. 가령 포도잔이 한 개만 주어졌을 경우에 dp[1]에만 값을 저장하고 끝나야 하는 것이죠. 따라서 dp[2]를 저장할 때는 N이 2 이상일 때에만 동작하도록 조건을 걸어주었습니다.
긴 풀이가 끝났습니다. 동적계획법 풀이 전략은 알면 알수록 재밌는 풀이 방법인 것 같습니다. :) 이제 좀 친해진 것 같네요
'개발 > DS&Algorithms' 카테고리의 다른 글
| [프로그래머스/JAVA] Level 1, 완주하지 못한 선수 (42576) (2) | 2022.10.17 |
|---|---|
| [백준] 깊이 우선 탐색_24479,24480_자바 (2) | 2022.08.11 |
| [백준] 프린터 큐_1966_자바 (2) | 2022.07.29 |
| [백준] 평범한 배낭 (DP)_12865_자바 (4) | 2022.07.03 |
| [알고리즘] 백트래킹(backtracking) 알아보기(& N-Queen 문제 풀이) (1) | 2022.06.20 |



