안녕하세요😎 백엔드 개발자 제임스입니다 :)
오늘은 백준의 문제 풀이를 포스팅하려고 합니다. 12865번에 해당하는 문제로, 동적 계획법의 대표적인 문제인 평범한 배낭입니다. 자세하게는 배낭 안에 어떤 물건들을 넣었을 때 최고의 가치를 갖는지 알아보는 문제입니다. 이러한 배낭 문제는 풀이법이 두 가지로 나뉩니다. 첫 번째는 물건을 쪼갤 수 있다고 가정했을 때입니다. 이때는 gready(탐욕) 알고리즘을 통해서 최적의 방법을 찾을 수 있습니다. 두 번째는 물건을 쪼갤 수 없을 때 사용하는 풀이 전략인 동적 계획법 전략입니다. 두 번째 풀이가 오늘 설명할 방식이죠. 이제 문제를 보면서 자세하게 설명하도록 하겠습니다.
https://www.acmicpc.net/problem/12865
12865번: 평범한 배낭
첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)
www.acmicpc.net
01. 동적 계획법
동적 계획법은 특별한 알고리즘이라기보다 문제를 푸는 전략과 동일합니다. 우리가 풀고자 하는 문제가 있다고 가정하겠습니다. 그것을 가장 큰 문제라고 했을 때, 먼저 해당 문제를 여러 개의 작은 문제로 나눕니다. 이어서 작은 문제의 결과를 저장한 뒤, 저장된 값들을 이용해서 풀고자했던 큰 문제를 해결합니다.
전에 동적 계획법에 대해서 다룬 적이 있습니다. 따라서 자세한 내용은 아래 링크를 참고해주시기 바랍니다.
[알고리즘] 동적 계획법(Dynamic Programming) 알아보기
안녕하세요😎 백엔드 개발자 제임스입니다 :) 이번에는 동적 계획법과 관련해서 포스팅하려고 합니다. 사실 동적 계획법은 어떠한 문제를 풀기 위한 전략 또는 기법에 가깝습니다. 따라서 추후
kang-james.tistory.com
02. 평범한 배낭 문제


* 요약
1) 물품의 수 N과 배낭의 무게 K 가 주어진다.
2) N개의 물건들은 각각 W 무게와 V 가치를 갖는다.
3) 무게 제한이 있는 배낭에 어떤 무게를 가진 물건들을 넣었을 때 나오는 최대의 가치를 구한다.
03. 풀이 아이디어
위에서 언급했듯이 각 물건들은 쪼갤 수 없으므로, 동적 계획법으로 풀이를 진행합니다. 사실 경우의 수를 모두 탐색해야 하는 브루트 포스 알고리즘과 유사하다고 할 수 있습니다. 단, 동적 계획법은 작은 문제에서 구한 결과값을 재사용하게 된다는 차이를 갖습니다.
아래에서 예시와 함께 설명하겠습니다. 이때 사용되는 예시는 백준에서 주어진 입출력의 예제를 사용해서 무게 제한이 7인 배낭과 [ 6, 4, 3, 5 ]의 무게를 가진 물건들로 가정하겠습니다.
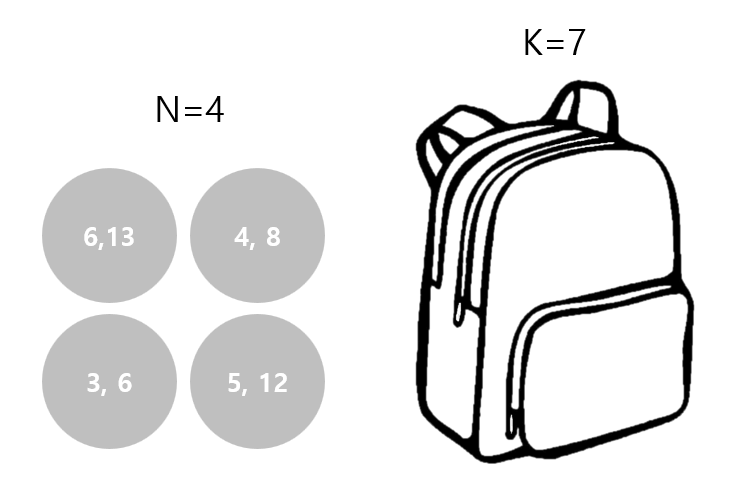
1) 4개의 물건 중 한 개를 배낭에 넣거나, 넣지 않습니다.
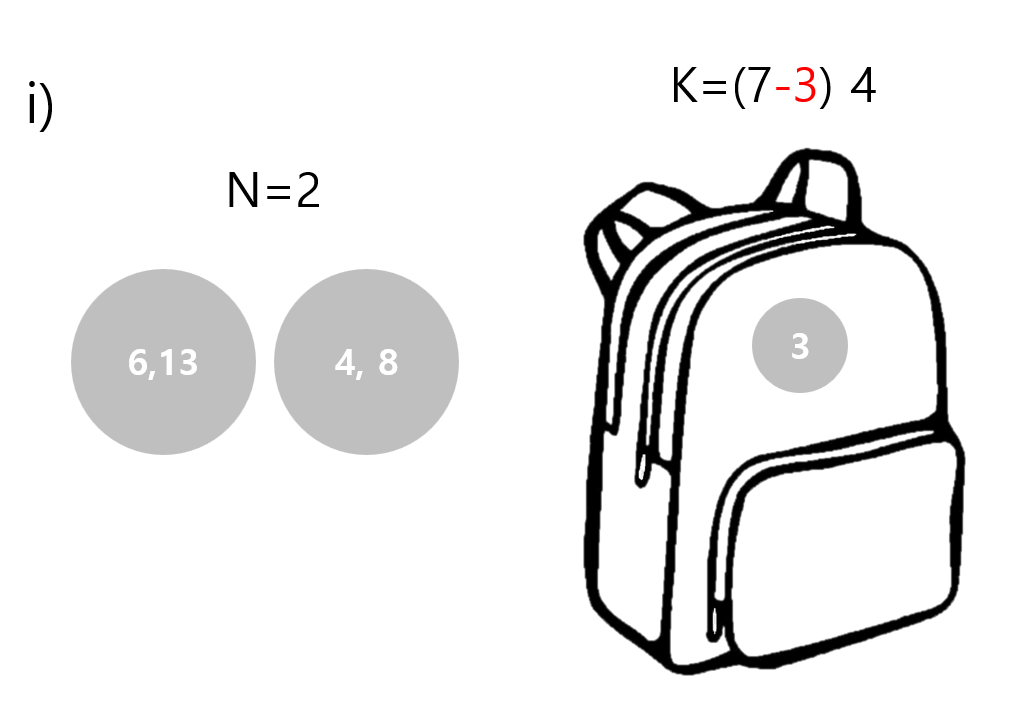
먼저 무게 5인 물건을 배낭에 넣거나, 넣지 않겠습니다. 그렇다면 아래 그림과 같이 두 가지 경우가 나올 것입니다.


보다시피 첫 번째 케이스는 무게 5인 물건을 배낭에 집어넣었기 때문에, 배낭의 제한 무게가 감소하게 됩니다. 즉, 7에서 5를 뺀 2가 남는 것입니다. 그리고 N은 물건 한 개를 제외하여 3이 된 것을 확인할 수 있습니다.
2) 3개의 물건 중 한 개를 배낭에 넣거나, 넣지 않습니다.
다음은 무게 3인 물건을 넣거나, 넣지 않아서 체크하도록 하겠습니다. 먼저 물건 5가 들어있는 배낭은 제한 무게가 2이기 때문에 무게 3인 물건을 넣을 수 없습니다. 따라서 아무것도 없는 배낭에 무게 3인 물건을 넣거나, 넣지 않은 케이스로 나눕니다. 그렇다면 아래 그림과 같은 결과가 나옵니다.
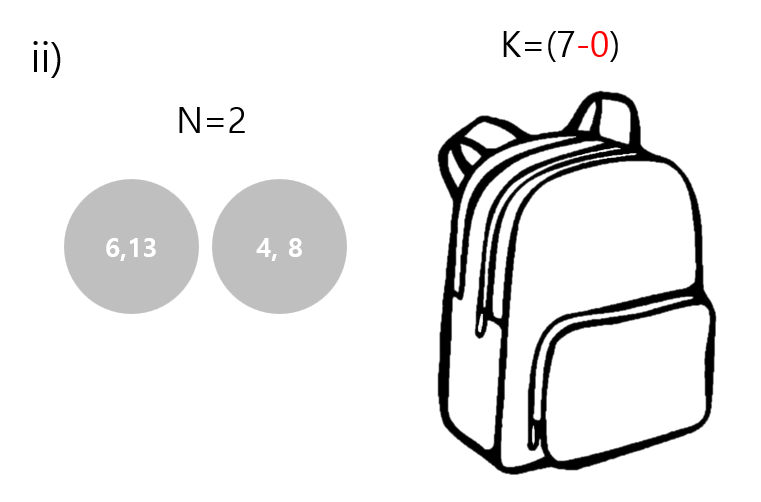
첫 번째 케이스는 물건을 넣었기 때문에 배낭의 제한무게가 4가 된 것을 볼 수 있습니다. 반면 두 번째 케이스는 물건을 넣지 않았기 때문에 무게에 변화가 없습니다. 이제 N은 물건을 한 개를 뺏기 때문에 2가 됩니다.
3) 2개의 물건 중 한 개를 배낭에 넣거나, 넣지 않습니다.
다음은 무게 4인 물건을 넣거나, 넣지 않을 건데요. 이번에는 경우의 수가 많아집니다. 그 이유는 무게 3인 물건이 들어있는 배낭에 다음 물건을 넣은 경우와 넣지 않은 경우, 아무것도 없는 배낭에 다음 물건을 넣거나, 넣지 않은 경우로 나누어지기 때문입니다.
이 과정이 끝나면 남은 물건도 동일하게 체크하는데요. 반복되는 과정이고, 경우의 수가 많아지기 때문에 생략하도록 하겠습니다.
다시 정리하면,
위 과정을 정리하도록 하겠습니다. 먼저 우리가 풀어야 했던 문제를 N<물건의 수>, K <제한 무게>라고 하겠습니다. 따라서 예제에 의해 (4,7)이 됩니다. 다시 말하면, 제한 무게가 7인 배낭에 4개의 물건이 있을 수 도 있고, 없을 수도 있다는 의미입니다. 이제 큰 문제를 작은 문제로 나눌 것입니다. 그 기준은 물건을 배낭에 넣었냐, 넣지 않았냐로 문제가 나뉘게 됩니다. 위에서 그림으로 알아봤듯이 물건을 하나씩 탐색할 때마다 N은 1씩 감소하고, 제한 무게는 배낭에 넣은 물건의 무게만큼 빼주게 됩니다. 이 과정을 트리 형태로 나타내면 아래와 같습니다.
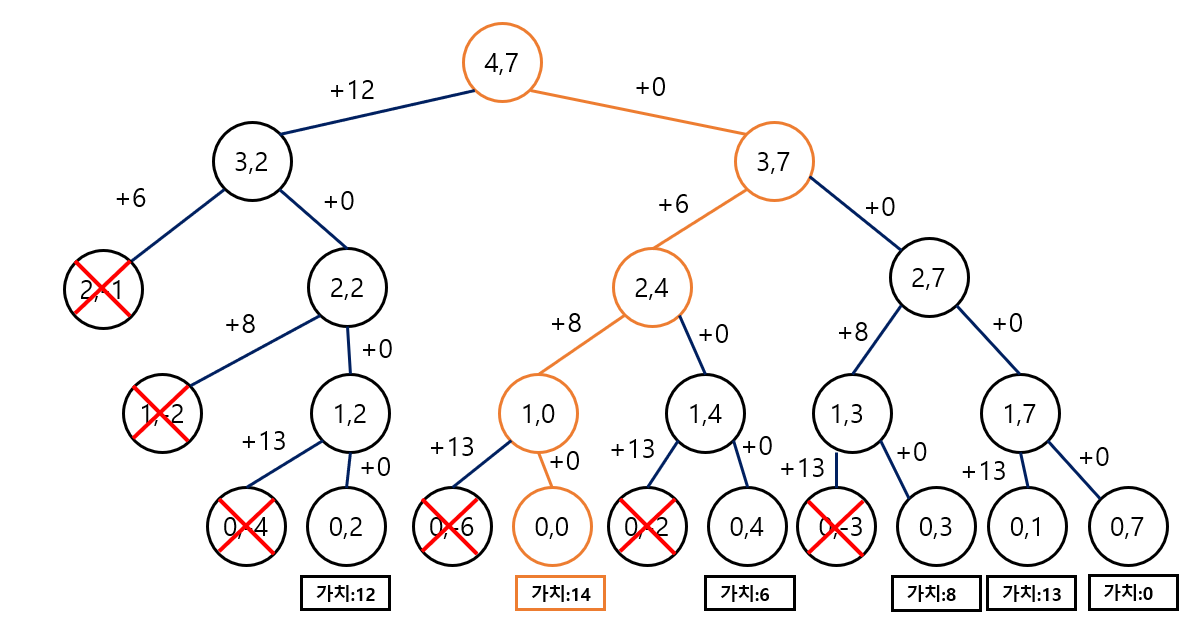
트리를 보면 좌측선은 물건을 넣은 경우, 우측선은 물건을 넣지 않은 경우에 해당합니다. 따라서 좌측선에서 해당 물건의 가치가 더해집니다. 물건을 모두 탐색하면서, 제한 무게를 넘어서지 않는 경우들을 찾고, 각 가치에서 최댓값을 구합니다. 결과는 배낭에 무게 3과 4인 물건을 넣었을 때 발생하는 가치 14가 최대 가치입니다.
우리는 여기서 점화식을 아래와 같이 표현할 수 있습니다.
Problem(N, K) = Max {
Problem(N-1, K - K [N]) + Value [N], (물건을 넣는 경우)
Problem(N-1, K) + 0 (물건을 넣지 않은 경우)
}
하지만 우리는 위 과정만 봤을 때는 동적 계획법의 전략이 들어간 게 맞는지 의문을 갖게 될 것입니다. 이렇게만 봤을 때는 브루트 포스(완전 탐색)와 다를 게 없어 보이는데요. 어떤 방식으로 문제를 풀어야 하는 것일까요?
04. 동적 계획법 풀이 전략 적용
해당 문제는 두 가지 방법으로 해결할 수 있습니다.
- Top - down 방식
- Bottom - up 방식

1) Top - down 방식
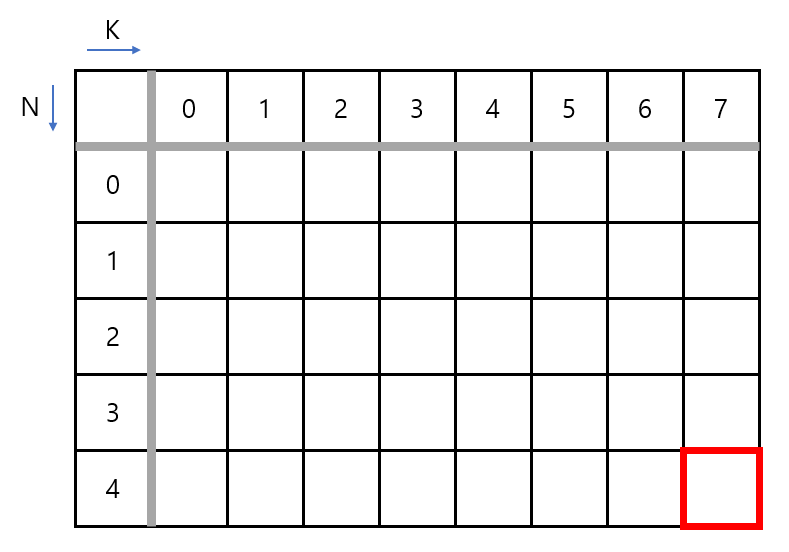
값들을 저장하기 위한 이차원 배열이 있습니다. 행의 인덱스는 배낭의 제한 무게, 열의 인덱스는 물건의 수를 의미하는데요.
해결하려는 문제는 이차원 배열의 인덱스 (4,7)에 해당합니다. 즉, 우리는 해당 부분의 가치가 몇인지 알아보는 것입니다.
Top - down 방식은 위에서 알아봤던 트리처럼 물건을 넣거나, 넣지 않은 경우를 고려하며 값을 필요로 하는 부분을 먼저 찾는 것입니다. 그렇게 N이 0이 됐을 때 (즉, 물건을 모두 체크한 경우), 반환 값을 가지고, 경로에 해당하는 가치들을 더하며, 최댓값을 구하고 문제를 해결하는 방법입니다. 이때 위에서 알아봤던 점화식에 따르게 됩니다.
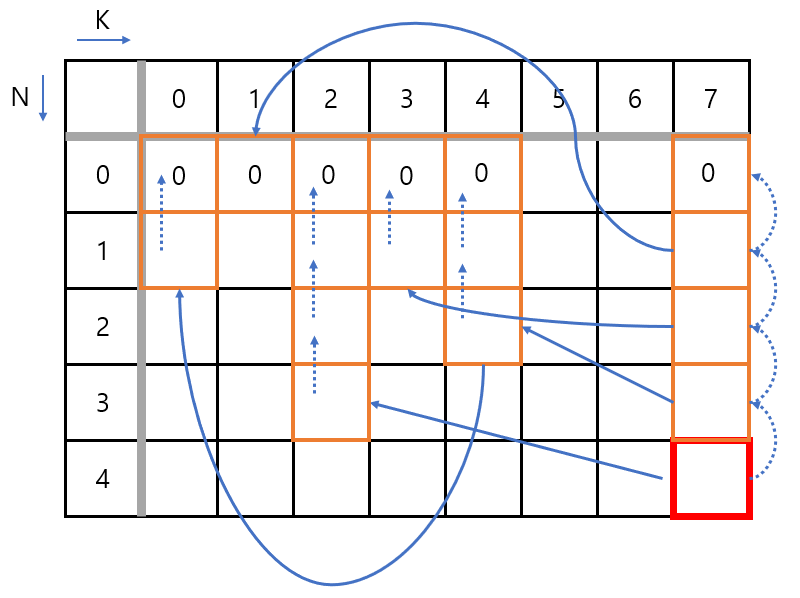
위 그림은 N이 0인 순간까지 탐색한 결과입니다. 물건의 수가 0이라면, 배낭의 무게 제한이 몇이든 가치는 0입니다.
이제 이 값을 가지고, 하위 문제로 왔던 경로대로 다시 올라가면서 가치의 최댓값을 찾습니다. 순차적으로 예를 들자면,
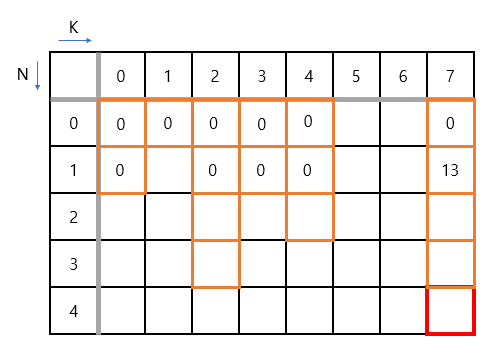
먼저 (1,0), (1,2), (1,3), (1,4)는 무게의 변화가 없기 때문에 각 위치에는 가치 0이 저장됩니다. 반면 (1,7)은 (0,1)과 (0,7) 두 가지의 경로를 갖습니다. 이때 (1,7)에서 (0,1)로 이동하는 경우는 무게 6인 물건을 배낭에 넣었다는 의미이기 때문에 가치 13이 발생합니다. 따라서 (0,1)과 (0,7)에서 (1,7)로 이동할 때 발생하는 가치 중 최댓값이 (1,7)에 저장하게 됩니다.
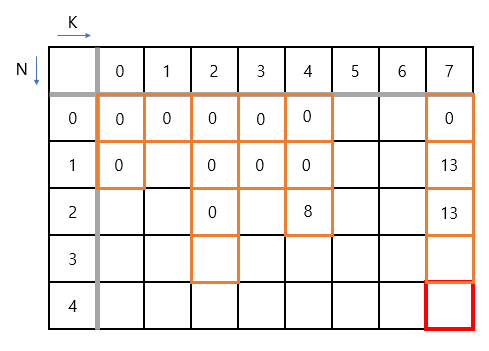
다음은 N=2일 때, 무게 4인 물건을 배낭에 넣거나, 넣지 않은 경우입니다. 먼저 K(제한 무게)가 2인 경우는 무게가 4인 물건을 배낭에 넣을 수 없기 때문에 그대로 0이 됩니다. K가 4일 때는 무게가 4인 물건을 배낭에 넣었을 경우 (1,0)의 가치에서 물건의 가치 8을 더한 값과 물건을 넣지 않았을 때의 가치 0을 비교하여 최댓값인 8이 저장됩니다. K가 7일 때는 무게 4인 물건을 넣었을 경우 (1,3)에 저장된 가치에서 가치 8을 더한 값과 물건을 넣지 않았을 때의 가치 13과 비교하여 최댓값인 13이 저장됩니다.
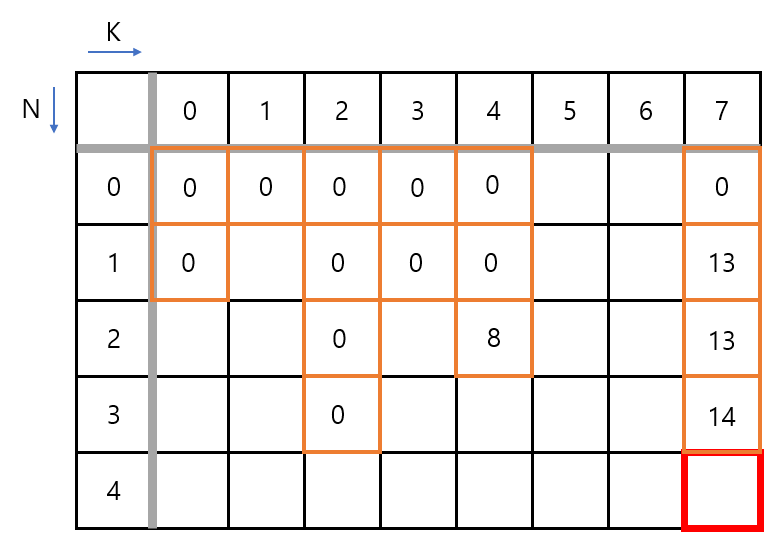
다음은 N=3일 때, 무게 3인 물건을 배낭에 넣거나, 넣지 않은 경우입니다. 이번에도 역시 K가 2일 때는 물건이 들어가지 않기 때문에 해당 위치의 가치는 0이 저장됩니다. 다음은 N이 7일 때입니다. 역시 무게 3인 물건을 넣었을 경우와 넣지 않은 경우 중 최댓값을 해당 칸에 저장하게 됩니다. 먼저 물건을 넣었을 경우는 (2,4)의 가치 8에서 물건의 가치 6이 더해진 14가 됩니다. 물건을 넣지 않은 경우는 (2,7)의 가치 13에서 0이 더해진 값 13이 됩니다. 따라서 더 큰 가치를 가진 3을 배낭에 넣은 경우의 결과값이 해당 위치에 저장되게 됩니다.
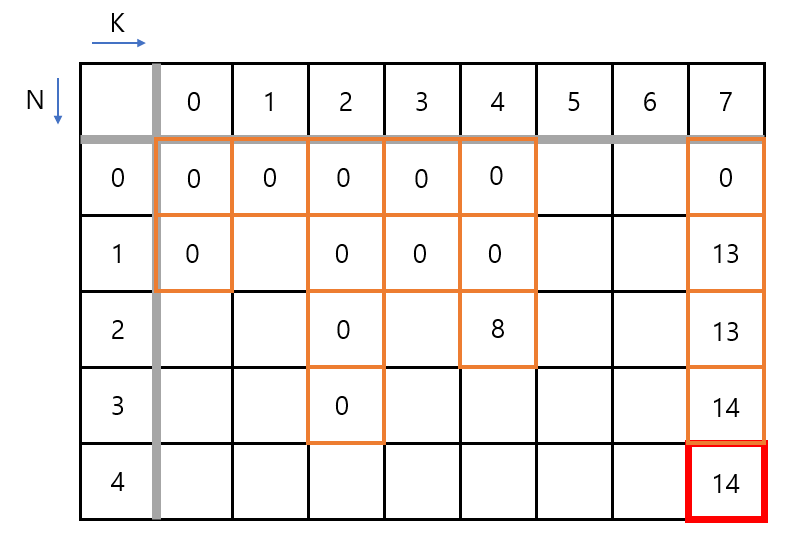
마지막으로 N이 4인, 무게 5인 물건을 넣거나, 넣지 않은 경우입니다. 첫 번째 물건을 넣은 경우 (3,2)의 가치 0과 물건의 가치 12가 더해져서 12가 되고, 두 번째 물건을 넣지 않은 경우는 3,7에서 가치 0을 더한 결과 14가 됩니다. 그리고 둘을 비교했을 때 14가 더 크므로 최종적으로 (4,7)에는 가치 14가 저장됩니다.
Top-down 방식 코드 적용
Top-down 방식은 재귀 풀이와 가깝습니다.
public class NormalBackpack_12865 {
static Integer[][] dpCase;
static int[][] stuff;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken()); // 물품의 수
int K = Integer.parseInt(st.nextToken()); // 버틸 수 있는 무게
// 이전 케이스의 결과를 저장해두기 위해 2차원 배열 생성
dpCase = new Integer[N][K+1];
// stuff
stuff = new int[N][2];
for(int i = 0 ; i < stuff.length; i++) {
st = new StringTokenizer(br.readLine());
stuff[i][0] = Integer.parseInt(st.nextToken()); // w
stuff[i][1] = Integer.parseInt(st.nextToken()); // v
}
System.out.println(ns(N-1,K));
}
// top-down 방식
public static int ns(int n, int k) {
// 물건이 0일 경우=> 더이상 담을 무게가 없기 때문에 가치 0 리턴
if(n < 0) {
return 0;
}
int currWeight = stuff[n][0];
int currValue = stuff[n][1];
if(dpCase[n][k] == null) {
// 현재 물건의 무게가 제한 무게보다 클 경우
// 가방 안에 포함시키지 않은 채 다음 물건으로 이동 -> 담지 않았기 때문에 value = 0;
// 즉 k는 그대로, n은 -1 진행
if(currWeight > k) {
dpCase[n][k] = ns(n-1, k);
} else {
// 점화식에 따라 나눈 문제들의 결과 중 max 값을 dpCase 배열에 저장
dpCase[n][k] = Math.max(ns(n-1 , k), ns(n-1, k - currWeight) + currValue);
}
}
return dpCase[n][k];
}
}2) Bottom - up 방식
Top-down 방식보다 좀 더 동적 계획법 전략에 가깝습니다.
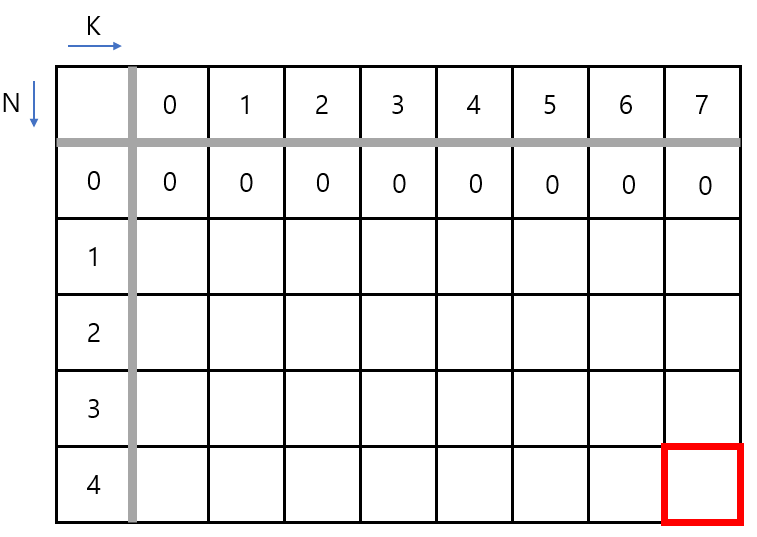
이번에도 역시 2차원 배열을 만들고, (4,7)의 저장될 가치를 찾는 것입니다. 여기서 열의 인덱스는 물건에 해당합니다. 즉, 인덱스 1번은 무게 6에 해당하며, 13이라는 가치를 갖습니다. 2,3,4 도 각각 { (4,8) , (3,6), (5,12) }를 갖고 있습니다. 0번 인덱스는 더미 데이터라고 생각하면 좋습니다. 단, 나중에 코드를 작성할 때 꼭 인덱스를 잘 신경 써야 합니다.
행은 이번에도 역시 배낭의 무게 제한입니다.
먼저 열의 0번 인덱스는 아무 물건도 없기 때문에 K의 값이 어떤 수가 오더라도 가치는 0입니다.
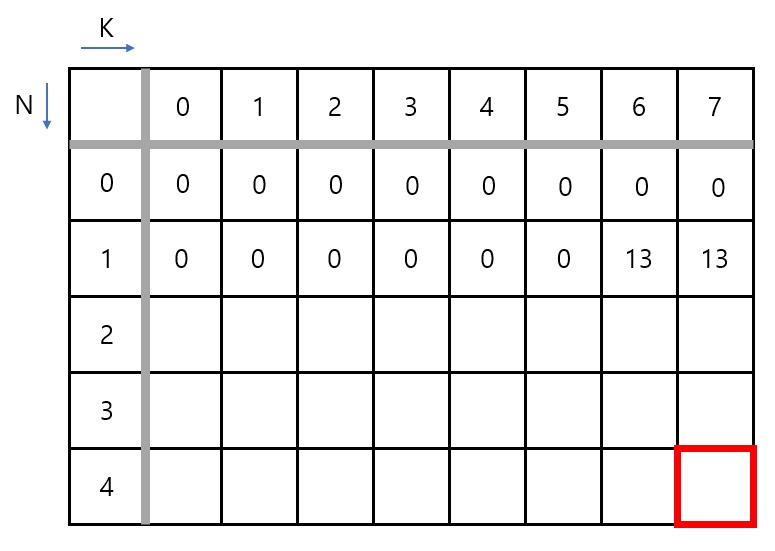
다음은 N이 1일 때입니다. 인덱스 1은 물건의 무게와 가치가 (6,13)에 해당합니다. 배낭의 제한 무게를 0부터 7까지 생각했을 때, 5까지는 무게 6인 물건을 넣을 수 없기 때문에 가치는 0입니다. 반면, 6과 7에는 물건을 넣을 수 있는데요. 이렇게 넣을 수 있을 때 물건을 넣는 경우와 물건을 넣지 않은 경우로 생각합니다.
첫 번째 물건을 넣는 경우, 배낭의 제한 무게 6에서 물건의 무게 6을 빼고 가치 13을 더합니다. 그럼 이제 제한 무게는 0이 되는데 이때 (0,0에 저장된 가치 값을 불러와서 13과 더합니다. 그럼 첫 번째 케이스는 13이 됩니다. 두 번째 물건을 넣지 않는 경우, (0,6)에 저장된 값과 0을 더하여 두 번째 케이스의 결과는 0이 됩니다. 이렇게 나온 첫 번째 케이스와 두 번째 케이스를 비교해서 최댓값을 해당 위치에 저장합니다. 따라서 (1,6)에는 13이 저장됩니다.
K가 7일 때도 동일합니다. 물건을 넣는다면 K에서 물건의 물건을 빼고, 이미 저장된 값을 불러와서 더합니다. 그리고 물건을 넣는 경우와 물건을 넣지 않은 경우를 비교하여 최댓값을 넣게 됩니다.
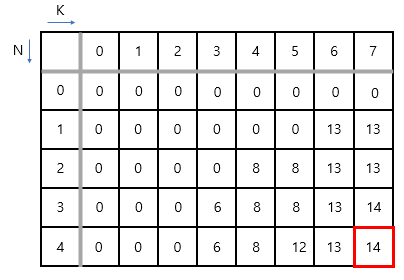
과정이 반복되기 때문에 생략하도록 하겠습니다. 위 그림이 최종 결과입니다. 결과값이나 문제를 나누는 기준 등 Top-down 방식과 Bottom-up 방식은 큰 차이가 없습니다. 다만 차이를 갖는다면, Top-down 방식은 하위로 문제를 나누다가 최하위에 도달했을 때 지나온 경로에 해당하는 가치들을 더한 후 최댓값을 구한 방식인 반면, Bottom-up은 최하의 문제들의 해답을 저장한 뒤, 상위 문제에서 하위에서 값을 활용하는 방식입니다.
아래에서 Bottom-up 방식으로 구현한 코드를 보도록 하겠습니다.
Bottom-up 방식 코드 적용
public class NormalBackpack3_12865 {
public static void main(String[] args) throws IOException, IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int N = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
int[] W = new int[N + 1]; // 무게
int[] V = new int[N + 1]; // 가치
int[][] dp = new int[N + 1][K + 1];
for (int i = 1; i <= N; i++) {
st = new StringTokenizer(br.readLine(), " ");
W[i] = Integer.parseInt(st.nextToken());
V[i] = Integer.parseInt(st.nextToken());
}
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= K; j++) {
// i번째 무게를 더 담을 수 없는 경우
if(W[i] > j) {
dp[i][j] = dp[i - 1][j];
}
// i번째 무게를 더 담을 수 있는 경우
else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - W[i]] + V[i]);
}
}
}
System.out.println(dp[N][K]);
}
}설명과 코드에서의 인덱스가 다소 차이가 있습니다.
코드 작성 시 신경 쓰고 작성하시기 바랍니다.
'개발 > DS&Algorithms' 카테고리의 다른 글
| [백준] 포도주 시식_2156_자바 (5) | 2022.08.10 |
|---|---|
| [백준] 프린터 큐_1966_자바 (2) | 2022.07.29 |
| [알고리즘] 백트래킹(backtracking) 알아보기(& N-Queen 문제 풀이) (1) | 2022.06.20 |
| [TIL] Daily Coding 회고 - 문자열 (2) | 2022.06.13 |
| [백준] 스택 수열_1874_자바 (2) | 2022.06.11 |



