안녕하세요😎 백엔드 개발자 제임스입니다 :)
오늘 알아볼 내용은 백트래킹(Backtracking) 알고리즘입니다. 해당 개념은 전에 다루었던, [동적 계획법과 분할 정복]과 동일하게 문제를 푸는 전략이라고 할 수 있습니다. 자세한 내용은 아래에서 다루도록 하겠습니다. 추가로 백트래킹의 대표적인 문제인 <N-Queen> 이라는 문제를 풀어보면서 더 자세하게 이해하도록 하겠습니다.
01. 백트래킹(Backtracking)
01) 백트래킹이란?
백트래킹은 모든 경우의 수를 고려하여 해를 찾는 방식입니다. 이름에서 유추할 수 있듯이, 퇴각 검색(추적)이라는 의미를 갖습니다. 즉, 해를 찾기 위해서 후보군을 나열하고, 제약 조건을 점진적으로 체크합니다. 만약 조건에 맞지않다면, 뒤로 돌아와서(backtrack), 바로 다음 후보군으로 넘어갑니다. 백트래킹에서 검색할 후보들을 상태 공간 트리(State Space Tree)로 표현합니다.
02) 상태 공간 트리(State Space Tree)
이번엔 상태 공간 트리를 예시로 해서 백트래킹을 이해하도록 하겠습니다. 방식은 루트 노드로부터 검색을 진행하게 됩니다. 중요한 것은 검색을 진행할 때마다 조건에 맞는 해인지 체크를 해야합니다.


보다시피 백트래킹은 트리 구조 기반으로 DFS(깊이 우선 탐색)를 진행합니다.


만약 조건에 부합하지 않다면, 더 이상 탐색을 진행하지 않습니다. 이후 위 그림처럼 이전 상태로 돌아간 뒤, 다음에 해당하는 노드를 검색합니다.


b의 자식 노드인 f도 조건에 맞지 않다면, b 이하는 모두 해가 될 수 없습니다. 따라서 이때는 a 상태로 돌아가서 c부터 다시 탐색을 진행합니다.
3) 백트래킹 관련 용어
- Promising : 해당 루트가 조건에 맞는지 검사하는 기법
- Pruning(가지치기) : 조건에 맞지 않으면 포기하고, 다른 루트로 바로 돌아서서 탐색의 시간을 절약
즉, 백트래킹은 트리 구조를 기반으로 DFS 방식을 진행하면서 각 루트에 대해 조건에 부합했는지 체크(Promising).
만약 해당 트리에서 조건에 맞지 않는 노드를 발견한다면, 더 이상 탐색을 멈추고, 다른 노드로 가지를 침(Pruning).
#요약
- 전반적인 문제 풀이 전략
- 퇴각 검색(backtrack)으로도 부름
- 제약 조건 만족 문제(Constraint Satisfaction Problem)에서 해를 찾기 위한 전략
- 상태 공간 트리(State Space Tree)로 표현
- 각 후보군을 DFS 방식으로 확인
02. N-Queen 문제 풀이
N-Queen 문제는 백트래킹의 대표적인 문제라고 할 수 있습니다. 여기서 퀸(Queen)은 우리가 아는 체스의 퀸과 동일합니다. 즉, NxN의 체스판(보드판)에 N개의 퀸을 두는 방법을 제시하는 것인데요. 이 때 배치할 퀸은 다른 배치된 퀸과 이동경로가 겹쳐서는 안 됩니다.
- NxN 크기의 체스판에 N개의 퀸을 서로 공격할 수 없도록 배치
- 퀸은 수직, 수평, 대각선으로 이동 가능

🙌 이런 조건에서 N이 4일 때, 4개의 퀸은 어떻게 배치할 수 있을까요?
(1) 4 x 4 체스판을 행과 열로 이루어진 테이블을 만듭니다.

(2) 가장 먼저는 행과 열이 0인 [0,0 지점]을 루트 노드로 탐색을 시작합니다.
0,0 부분에 퀸을 배치했다고 가정합니다.
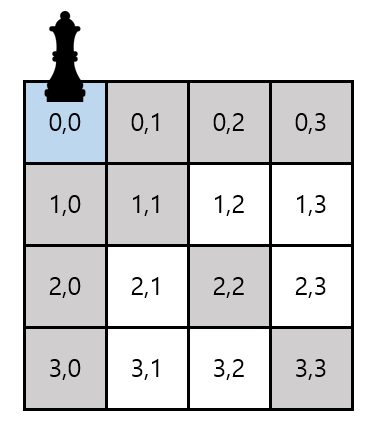
* 회색 칸은 조건에 따라 다음 퀸을 배치할 수 없는 위치입니다. (퀸의 이동 경로)
조건에 따라 다음 퀸은 이미 배치된 퀸과 같을 열에 위치할 수 없습니다. 즉, 다음 퀸은 1번 열 중에 배치해야 합니다. 이제 1,0부터 1,3을 순차적으로 체크합니다. 퀸의 이동방향이 수직 또는 대각선이기 때문에 1,0과 1,1에는 다음 퀸을 배치할 수 없습니다. 그렇다면 남은 1,2와 1,3에 배치할 수 있겠죠?
(3) [1,2 지점]에 두 번째 퀸을 배치합니다.

위 그림은 열 1, 행 2에 해당하는 위치에 두 번째 퀸을 둔 모습입니다. 이제 세 번째 퀸을 배치하기 위해서 다음 열인 2번 열을 0행부터 3행까지 탐색을 진행합니다. 하지만 그림을 보다시피 이미 앞에서 둔 퀸들로 인해서 세 번째 퀸을 배치할 수 없게 되었습니다.
드디어 백트래킹이 진행됩니다. 1,2 위치는 잘못된 위치란 것을 알았습니다. 따라서 두 번째 퀸을 1,2에서 제거하고, 1,3으로 이동합니다. 이어서 똑같이 가지를, 치고 탐색을 진행합니다.
(4) [1,2 지점]의 퀸을 제거하고, [1,3 지점]에 두 번째 퀸을 배치합니다. 동일한 방법으로 더 이상 퀸을 둘 수 없거나, 모두 둘 때까지 진행합니다.

[0,0 지점]을 노드로 한 경우는 3번 열에서 퀸을 배치할 수 없게 됩니다. 즉, 0,0 지점에 퀸을 배치하는 것부터 잘못된 것입니다. 동일하게 첫 번째 퀸을 옆 칸인 0,1로 이동시킵니다. 이어서 똑같이 진행합니다.
원리는 어느 정도 알았을 것이라 생각되어, 마지막으로 해의 일부인 상황을 보도록 하겠습니다.
(5) [0,1 지점]을 루트 노드로 탐색을 진행

위에서 설명한 방법으로 조건에 맞게 반복적으로 탐색을 진행합니다. 다양한 해가 나올 텐데 그중, 위 그림이 첫 번째 결과에 해당합니다.
🙌 조건에 부합하는지 판별하는 방법
지금까지 N-Queen 문제에서 적용되는 백트래킹의 원리에 대해서 이해했습니다. 해당 문제를 코드로 풀어보기 전에, 퀸을 배치할 때 조건에 부합한 위치인지는 어떻게 판별할 수 있을까요?
#1 수평
같은 열에 있으면, 퀸이 수평으로 이동할 수 있는 위치입니다.
하지만 우리는 코드를 작성할 때, 해당 열에 퀸을 배치하면 다음 퀸은 무조건 다음 열에 배치하도록 할 것입니다. 즉, 우리는 수직 또는 대각선 위치인지만 체크하면 됩니다.
#2 수직
같은 행에 있으면, 퀸이 수직으로 이동할 수 있는 위치입니다.

위 그림처럼 배치했던 퀸들의 행과 같은 행인지 체크합니다.
#3 대각선
X2 - X1 = |Y1-Y2| (X= 열, Y=행)

현재 퀸은 0번 열, 1번 행인 [0,1 지점]에 위치합니다. 1번 열에서 대각선 위치는 [1,0]과 [1,2]에 해당합니다.
여기서 특징은 대각선 위치의 열에서 현재 퀸의 열을 뺀 값과 대각선 위치의 행에서 현재 퀸의 행을 뺀 값의 절댓값이 같다는 것입니다.
(열) 1 - 0 = (행) |2 - 1| or (열) 1-0 = (행) |0 - 1|
2번 열도 동일합니다. 이를 일반화하여 식으로 나타내 보겠습니다. 현재 퀸의 열을 X1, 행을 Y1 이라 하고, 대각선 위치의 열을 X2, 행을 Y2라 한다면, 결과는 X2 - X1 = |Y1-Y2| 가 됩니다. (절댓값이기 때문에 피연산자의 위치는 상관없습니다.)
🙌 코드로 작성하기
이제 문제 풀이 내용에 대한 코드를 작성하겠습니다. 백트래킹은 대체로 재귀, 스택, for 등으로 문제를 해결할 수 있습니다. 저는 여기서 재귀를 활용해서 풀도록 하겠습니다.
import java.util.ArrayList;
public class NQueenProblem {
public static void main(String[] args) {
NQueenProblem nObject = new NQueenProblem();
nObject.dfsFunction(4, 0, new ArrayList<Integer>());
}
/**
*
* @param N : 체스판 크기, 배치할 퀸의 개수
* @param row : 퀸을 배치하기 위해 탐색할 열
* @param currentQueen : 현재 배치된 퀸들의 행을 저장한 배열
*
* 재귀로 함수를 시작할 때마다 row +1 -> 다음 열 탐색
* */
public void dfsFunction(Integer N, Integer currentRow, ArrayList<Integer> currentCandidate) {
// 보드판의 마지막까지 순회하여, 퀸의 위치를 다 찾았을 때
if(currentRow == N) {
System.out.println(currentCandidate);
return;
}
for(int column =0; column < N; i++) {
// 현재 열과 행에 queen 을 배치할 수 있는지 체크
if(this.isAvailable(currentCandidate, column)) {
// 현재 행을 배열에 추가 (index가 열에 해당)
currentCandidate.add(column);
// 현재 열에 퀸을 찾으면 다음 열 검색
this.dfsFunction(N, currentRow+1, currentCandidate);
// Pruning(가지치기) 기법 : 조건에 부합하지 않다면, 이전 케이스를 제거하고, 다음 노드 탐색
currentCandidate.remove(currentCandidate.size() - 1);
}
}
}
/**
* @param column : 퀸을 배치하기 위해 탐색할 열
* @param currentQueen : 현재 배치된 퀸들의 행을 저장한 배열 (index 는 열과 동일)
* @return 지금까지 저장된 퀸들의 수직 또는 대각선 위치라면 false 반환 (아니라면 true)
*/
public static boolean isAvailable(ArrayList<Integer> candidate,int currentCol) {
int currentRow = candidate.size(); // 배열의 사이즈는 현재 탐색할 열과 동일
for(int i = 0; i < currentRow; i++) {
// Promising(조건) 기법
// 퀸의 위치가 될 수 없는 조건
// 1) 열이 같을 때(수직일 때) -> y1 == y2
// 2) 현재 퀸을 두려는 열에서 이미 퀸을 둔 자리의 열을 뺀 값이 서로의 행을 뺀 값과 같을 때 -> |y1-y2| == x2-x1
if (currentCol == candidate.get(i) || Math.abs(candidate.get(i) - currentCol) == currentRow - i) {
return false;
}
}
return true;
}
코드에 주석을 추가하다 보니, 코드 길이가 굉장히 길어졌습니다. 위에서 설명한 대로, 재귀를 통해서 탐색을 진행했습니다.
'개발 > DS&Algorithms' 카테고리의 다른 글
| [백준] 프린터 큐_1966_자바 (2) | 2022.07.29 |
|---|---|
| [백준] 평범한 배낭 (DP)_12865_자바 (4) | 2022.07.03 |
| [TIL] Daily Coding 회고 - 문자열 (2) | 2022.06.13 |
| [백준] 스택 수열_1874_자바 (2) | 2022.06.11 |
| [백준] 수 정렬하기 3_ 10989_자바 (2) | 2022.06.07 |



