03. 정렬 알고리즘(2)
저번에는 정렬 알고리즘에서 O(N^2)의 수행속도로를 갖는 방식 3가지(버블, 삽입, 선택)에 대해서 알아봤습니다.
이번에는 O(logN)의 수행속도를 갖는 정렬에 대해서 알아볼 것인데요.
O(logN) 정렬들은 앞에서 알아본 정렬들과 다르게 '검색 범위가 점점 감소하는 방식'이라는 큰 특징을 갖습니다.
1) 퀵 정렬
퀵 정렬은 배열에서 한 수를 기준으로 작은 수와 큰 수를 재배치 하는 방법입니다.
여기서 기준을 피봇(PIVOT)이라고 합니다.
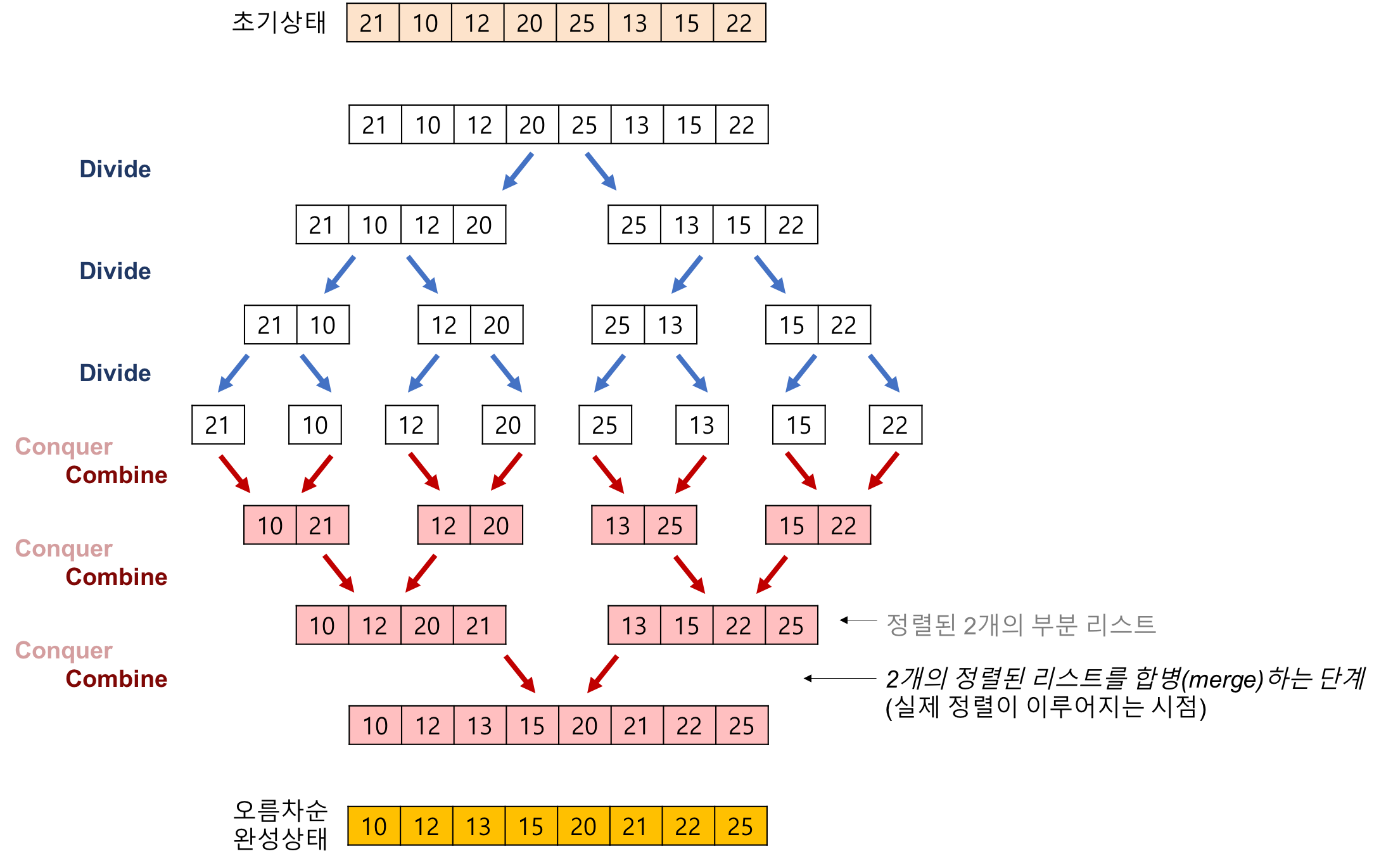
2) 병합(합병) 정렬
- 분할(Divide) : 하나의 리스트를 균등하게 두 개의 리스트로 분할합니다.
- 정복(Conquer) : 분할된 부분 배열을 정라합니다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출을 이용하여 다시 분할 정복 방법을 적용합니다.
- 결합(Combine) : 정렬된 부분 배열들을 하나의 배열에 합병합니다.

3) 힙 정렬
힙은 '최솟값 또는 최댓값을 빠르게 찾아내기 위해 완전이진트리 형태로 만들어진 자료구조' 입니다.
주로 우선순위를 나타낼 때 활용합니다.

위에서 언급했듯이 항상 complete binary tree를 유지해야합니다. 그 말인 즉슨 부모 노드를 출력을 하면, 트리는 재정렬을 통해서 형태를 갖춰야 하는 것입니다. 반대로 새로운 노드를 삽입할 때도 마찬가지입니다.
힙 정렬은 실제로는 배열로 많이 구현합니다.
이진 트리에서 가장 위에 있는 노드가 가장 작은 수라면 min heap, 가장 큰 수라면 max heap이라고 합니다. 그리고 여기서 만약 min heap으로 정렬한다면, 하위에 위치한 자식노드는 부모 노드보다 큰 숫자를 가져야 합니다.
(max heap이라면, 부모 노드가 자식 노드보다 커야겠죠?)
1) Heap은 배열로 구현을 많이 합니다.
2) 배열에서 부모 노드는 자식 노드의 1/2 인덱스에 위치합니다.
3) Heap 구현시 배열의 0번 인덱스는 잘 사용하지 않습니다.
4) 우선순위 큐(Priority Queue)를 구현할 때 Heap을 활용합니다.
◆ Heap 정렬 코드 예제
public class HeapSort {
private int SIZE; //힙의 사이즈
private int heapArr[]; // 베열로 구현하는 힙
public HeapSort() { // 생성자 초기화
SIZE = 0;
heapArr = new int[50] // 50크기의 배열 생성
}
// 힙 배열에 숫자 삽입 메소드
public void insertHeap(int input) {
int i = ++SIZE;
//min heap 구현 방법
// 힙 내의 다른 수가 있는지 판단 및 집어 넣은 수가 부모노드보다 작은지 판단
while((i != 1) && (input < heap[i<2])) {
heapArr[i] = heapArr[i/2]; // min heap에서 부모 노드가 자식보다 작아야 하므로 만약 부모가 크다면 자식과 위치 변경
i= i/2; // 부모 노드 위치
}
heapArr[i] = input;
}
// 힙 배열에서 숫자 추출 메소드
public int getHeapSize() {
return SIZE;
}
public int deleteHeap() {
int parent, child;
int data, temp;
data = heapArr[1];
temp = heapArr[SIZE];
SIZE -= 1;
parent = -1;
child = 2;
while(child <= SIZE) {
if((child<SIZE) && (heapARr[child] > heapArr[child+1])) {
child++;
}
if(temp <= heapArr[child]) break;
heapArr[parent] = heapArr[child];
parent = child;
child *= 2;
}
heapArr[parent] = temp;
return data;
}
public void printHeap() {
System.out.printf("\n Min Heap : ");
for(int i =1; i<=SIZE; i++) {
System.out.printf("[%d]", heapArr[i]);
}
}
public static void main(String[] args) {
HeapSort h = new HeapSort();
h.insertHeap(80);
h.insertHeap(50);
h.insertHeap(70);
h.insertHeap(10);
h.insertHeap(60);
h.insertHeap(20);
h.printHeap();
int n, data;
n=h.getHeapSize();
for(int i=1;i<=n;i++) {
data = h.deleteHeap();
System.out.printf("\n 출력 : [%d]", data);
}
}
}◆ 출력 예시


1) 최상위의 노드인 10을 추출한 후 가장 하위에 노드가 올라옵니다.
2) 다음 child 노드 중 더 작은 값을 찾고 방금 올라온 parent 노드와 비교를 합니다. 만약 parent 노드가 자식 노드보다 크다면 위치를 바꿉니다.
3) 위 이미지에서 보면 다음으로 20이 추출됩니다.
4) 이와 같이 반복하며 모두 출력합니다.
◆ 결과
[0], [10], [20], [50], [60], [70], [80]
'개발 > DS&Algorithms' 카테고리의 다른 글
| [백준] ACM 호텔_10250_자바 (0) | 2022.02.11 |
|---|---|
| [백준] 알파벳 찾기_10809_자바 (6) | 2022.02.05 |
| [백준] 최소,최대_10818_자바 (6) | 2022.02.01 |
| [백준] 평균은 넘겠지_4344_자바 (2) | 2022.01.31 |
| [백준] 서로 다른 나머지 개수 구하기_3052_자바 (4) | 2022.01.30 |



