안녕하세요😎 백엔드 개발자 제임스입니다 :)
오늘 알아볼 내용은 그래프(Graph) 입니다. 먼저 그래프란 이름을 들으니 무엇이 떠오르나요?


대부분의 사람들은 위 그림과 같은 모습을 생각할 것입니다. 오늘 포스팅할 그래프는 마치 복잡한 네트워크처럼 그물망으로 이루어진 자료구조입니다. 위 그림과는 다른 형태죠. 이제 아래에서 자세하게 알아보도록 하겠습니다.
1. 그래프(Graph)란?

위에서 언급했듯이 그래프(Graph)는 어떠한 정점들을 그물망처럼 연결하여 나타낸 자료구조입니다. 그래프에 대해서 쉽게 이해할 수 있도록 먼저 용어를 알아보겠습니다.
1) 그래프의 용어
- 정점(Vertex) : 하나의 점을 의미합니다. 또는 위치가 될 수 있습니다. 위에 자료구조 그래프 예시에서 주황색 원에 해당합니다. 정점을 다른 말로는 노드(Node)라고도 합니다.
- 간선(Edge) : 정점과 정점을 연결하는 선입니다. link, branch 라고도 합니다.
- 기타 용어
- 인접 정점(Adjacent Vertex) : 한 정점에서 간선으로 연결된 정점들을 말합니다.
- 정점의 차수(Degree) : (무방향 그래프에서) 하나의 정점에 인접한 정점의 수입니다.
- 진입 차수(In-Degree) : (방향 그래프에서) 외부에서 오는 간선의 수입니다.
- 진출 차수(Out- Degree) : (방향 그래프에서) 외부로 향하는 간선의 수입니다.
- 경로 길이(Path Length) : 경로를 구성하기 위해 사용된 간선의 수입니다.
- 단순 경로(Simple Path) : 처음 정점과 끝 정점을 제외하고, 중복된 정점이 없는 경로입니다.
-> ex) A -> B -> C : 단순 경로 / A -> B -> C -> B -> A -> D -> E : 단순 경로 X - 사이클(Cycle) : 단순 경로의 시작 정점과 종료 정점이 동일한 경우를 의미합니다.
2) 그래프의 종류
#1 무방향 그래프와 방향 그래프
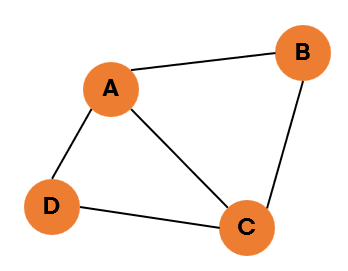
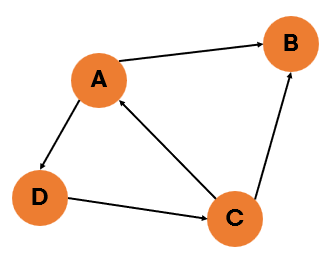
| 무방향 그래프 | 방향 그래프 |
| 방향이 없는 그래프 | 간선에 방향이 있는 그래프 |
| 양방향으로 이동할 수 있음 | 화살표로 표기된 방향으로만 이동 가능 |
| 보통 정점 A, B가 연결되어 있을 경우 (A,B) 또는 (B,A)로 표기 | A 에서 B로 향하는 간선일 경우, <A,B>로 표기 (<B,A>로 표기 X) |
#2 가중치 그래프(Weighted graph)

- 네트워크(Network)
- 간선에 비용 또는 가중치가 할당된 그래프
- 예를 들어 정점과 정점 사이에 발생하는 시간, 거리가 될 수도 있음
#3 연결 그래프(Connected graph)와 비연결 그래프(Disconnected graph)
- 연결 그래프 : 무방향 그래프에서 모든 정점에 대해 항상 경로가 존재하는 경우
- 비연결 그래프 : 무방행 그래프에서 특정 정점에 대해 경로가 존재하지 않는 경우
#4 사이클(Cycle)과 비순환 그래프(Acyclic graph)
- 사이클 : 단순 경로의 시작 정점과 종료 정점이 동일
- 비순환 그래프 : 사이클이 없는 그래프
#5 완전 그래프(Complete graph)
- 모든 정점이 연결된 상태
3) 그래프와 트리 비교하기!
트리(Tree) 자료구조는 그래프 자료구조에 속한 특별한 종류!
트리는 그래프에 속하는 자료구조입니다. 따라서 트리도 그래프와 유사하게 서로 다른 노드에 선들로 연결되어 있죠. 단, 몇가지 차이점을 갖습니다.
| 그래프 | 트리 |
| 노드와 노드를 연결하는 간선으로 표현되는 지료구조 | 그래프의 한 종류, 방향성이 있는 비순환 그래프 |
| 방향 그래프, 무방향 그래프 등 다양한 그래프 존재 | 방향 그래프만 존재 |
| 사이클, 순환, 비순환 그래프 존재 | 비순환 그래프로 사이클이 존재하지 않음 |
| 루트 노드가 존재하지 않음 | 루트 노드가 존재 |
| 부모 자식 개념이 존재하지 않음 | 부모 자식 관계가 존재 |
2. 그래프 탐색 알고리즘, BFS와 DFS 알아보기
BFS, DFS는 대표적인 그래프 탐색 알고리즘
1) BFS(Breadth-First Search)
BFS는 우리 말로 너비 우선 탐색입니다. 정점들과 같은 레벨에 있는 정점들을 먼저 탐색하는 방식입니다. 여기서 같은 레벨은 현제 정점(노드)을 의미합니다. 따라서 아래 그림과 같은 순으로 탐색을 진행하는 것이죠.

즉, 너비 우선 탐색은 시작 정점(V)에서 한 단계씩 내려가면서, 해당 정점과 같은 레벨에 있는 정점들을 먼저 순회하합니다. 형제 정점들을 모두 탐색했으면, 다음 레벨로 내려갑니다. 여기서 정점으로 이동할 때, 꼭 선을 타고 인접 정점으로만 이동해야하나 하고 오해할 수 있습니다. 컴퓨터 세계에서는 그렇지 않습니다. 최소 해당 탐색 방식에서는 B 에서 C로 이동하는 방식이 허용되죠.
BFS 탐색 : A -> B -> C -> D -> G -> H -> I -> E -> F -> J
2) DFS(Depth-First Search)
DFS는 우리 말로 깊이 우선 탐색입니다. 해당 탐색은 이름처럼 세로 방향으로 우선 탐색하는 방법입니다. 즉, 자식 노드들을 모두 탐색한 뒤, 다시 부모 노드로 올라오고, 이어서 남은 형제 노드로 이동하여 또 세로로 탐색을 진행하죠. 그림으로 보면 아래와 같습니다.


A 정점에서 다음 정점으로 B 정점과 C 점정 무엇이와도 상관 없습니다. 단, 위 그림처럼 다음 정점의 자식정점으로 탐색을 진행해야 합니다. 다시 말해서 B 정점으로 간다면, 다음 D -> E -> F 방향이고, C 정점으로 간다면, I -> J -> H 방향이 되어야 하죠.
추가로 BFS와 DFS 모두 중요한 특징이 있습니다. 그것은 한번 지나고 간 정점은 다시 지나지 않는 것이죠.
DFS 탐색 : A -> B -> D -> E -> F -> C -> G -> H -> I -> J
(또는 A -> C -> I -> J -> H -> G -> B -> D -> F -> E)
3) BFS와 DFS 코드 구현
* 너비 우선 탐색(BFS)는 큐를 활용합니다.
* 깊이 우선 탐색(DFS)는 스택을 활용합니다.

코드를 구현하기 전에 위 그림에 대한 정보를 HashMap에 저장할 수 있는데요. 각 정점들을 KEY에 저장하고, 해당 KEY와 연결된 정점들을 VALUE에 저장합니다.

#1 BFS 코드 구현
public ArrayList<String> bfsFunc(HashMap<String, ArrayList<String>> graph, String startNode) {
ArrayList<String> visited = new ArrayList<String>(); // ArrayListQueue1
ArrayList<String> needVisit = new ArrayList<String>(); // ArrayListQueue2
needVisit.add(startNode);
int count = 0; // 시간 복잡도 체크용 변수
// needVisit의 사이즈가 0보다 크면, 아직 방문할 곳이 남았다는 뜻
while (needVisit.size() > 0) {
count += 1;
//현재 방문해야할 리스트에 가장 앞에 있는 값을 꺼낸다.
String node = needVisit.remove(0);
// 이미 방문을 한 곳인지 체크 -> 하지 않았다면 조건 실행
if (!visited.contains(node)) {
visited.add(node);
needVisit.addAll(graph.get(node));
}
}
System.out.println(count); // 시간 복잡도 체크
return visited;
}- BFS 에서는 두 개의 큐를 사용합니다.
- Queue 패키지도 있지만, 여기서는 ArrayList<>()로 구현했습니다.
- 따라서 visited와 neddVisit인 두 개의 큐를 생성했습니다.
- 메서드의 매개 변수로 그래프 정보가 담긴 HashMap과 시작 정점을 받습니다.

이 처럼 ArrayList를 통해서 두 개의 큐를 만들었습니다. 이제부터 방문이 필요한 정점을 neeVisit에 넣고, 방문한 정점을 visited에 추가할 것입니다. (1) 가장 먼저 매개변수로 받은 start 정점의 데이터를 needVisit에 넣습니다. 이제 needVisit에 값이 있기 때문에 탐색을 시작합니다.

(2) 큐의 정책에 따라서 needVisit에서 A를 꺼냅니다. (3) 그리고 visited에 값이 있는지 체크합니다. 그 이유는 그래프에서는 한번 지났던 곳은 또 지나지 않기 때문이죠. 아직 A를 지나지 않았기 때문에 visited에 넣습니다. (4) 다음은 HashMap에서 키 A에 해당하는 값들을 needVisit에 넣습니다. 따라서 B와 C가 들어간 것을 볼 수 있죠.

아직 방문해야할 정점들이 있기 때문에 아까와 같은 탐색을 반복합니다. (5) 이번에도 큐의 정책에 따라서 B를 꺼냅니다. (6) B는 visited에 없기 때문에 데이터를 추가합니다. (7) B에 해당하는 해시값들을 needVisit에 넣습니다.
이와 같이 needVisit의 길이가 0이 될때까지 탐색을 진행합니다. 모두 마쳤다면, visited은 아래와 같이 됩니다.

#2 DFS 코드 구현
public ArrayList<String> dfsFunc(HashMap<String,ArrayList<String>> graph, String start) {
ArrayList<String> needVisit = new ArrayList<>(); // 스택으로 진행
ArrayList<String> visited = new ArrayList<>(); // 큐
needVisit.add(start);
while(needVisit.size() > 0) {
// 스택 정책에 따라서 마지막 인덱스 값 추출
String node = needVisit.remove(needVisit.size()-1);
if(!visited.contains(node)) {
visited.add(node);
needVisit.addAll(graph.get(node));
}
}
return visited;
}- DFS는 visited는 동일하게 큐지만, needVisit은 스택으로 진행합니다.
- 따라서 needVisit에서 데이터를 꺼낼 대 제일 마지막에 있는 값을 꺼냅니다.

DFS도 needVisit에 start 정점의 값을 넣은 후 탐색을 시작합니다. 그리고 BFS와 동일하게 추출 후 visited에 값이 있는지 체크를 한 뒤 추가하고, 키 A에 해당하는 값들을 needVisit에 넣습니다.
이제부터가 중요합니다.

이번에 needVisit은 stack으로 활용되기 때문에, B가 아닌 C가 나오게 됩니다. 역시나 visited에 값이 있는지 체크를 합니다. 방문한 적이 없다면, visited에 C를 추가하고, 키 C의 해당하는 값들인 G, H, I를 needVisit에 추가합니다.
다음 탐색에서도 B가 아닌, 마지막 인덱스에 해당하는 I를 꺼내게 됩니다. 이러한 방식으로 더 이상 탐색할 정점이 없다면, 아래와 같은 결과가 나오게 됩니다.

4) 시간 복잡도
시간 복잡도 : O(V+E)
일반적으로 BFS 그래프 알고리즘과 DFS 그래프 알고리즘은 while의 반복수에 따라서 시간 복잡도가 결정됩니다.
정점(노드) 수를 V, 간선 수를 E라고 했을 때, while은 V + E 만큼 반복을 수행합니다. 따라서 시간 복잡도는 O(V+E)가 됩니다.
'개발 > DS&Algorithms' 카테고리의 다른 글
| [백준] 스택 수열_1874_자바 (2) | 2022.06.11 |
|---|---|
| [백준] 수 정렬하기 3_ 10989_자바 (2) | 2022.06.07 |
| [알고리즘] 병합 정렬(Merge sort) 알아보기 (6) | 2022.05.11 |
| [알고리즘] 분할 정복(Divide and Conquer) 알아보기 (8) | 2022.05.10 |
| [알고리즘] 동적 계획법(Dynamic Programming) 알아보기 (3) | 2022.05.07 |



