11729번 Java - 하노이 탑 이동 순서
이번 문제의 분류는 <재귀>에 해당합니다.
하노이 탑 관련 문제는 재귀의 대표라고 할 수 있습니다.
저는 하노이 탑 원리를 알고 있으면서도, 알고리즘을 구현하는 것이 쉽지 않았습니다.
따라서 이렇게 정리합니다.
시작하기에 앞서서 재귀에 대해서 정리해보도록 하겠습니다.
재귀 함수란?
자기 자신을 호출하는 함수로 종료조건이 충족될 때까지 주어진 작업을 수행하는 것입니다.
팩토리얼을 구하는 문제로 재귀 함수 예시를 들겠습니다.
팩토리얼이란?
하나의 자연수 n이 주어졌을 때, 1부터 n 까지 모든 자연수의 곱을 말합니다.
기호로 표시하면, n! 라고 나타냅니다.
다시 말해서 5!을 구하면, 1 X 2 X 3 X 4 X 5 가 되면서 결과는 120이라는 값을 얻습니다.
이제 재귀함수를 활용해서 코드를 작성해보겠습니다.

N이라는 변수에 우리가 구하고자하는 값을 입력합니다.
그리고 팩토리얼을 구해줄 함수 f( )를 만듭니다. 이 함수가 재귀함수가 됩니다.
내부를 보면, else 부분에 또 한번 함수가 호출되는 것을 볼 수 있습니다. 단, N-1을 인자로 넣고 있습니다.
이처럼 자기 자신을 호출하는 것입니다.
여기서 중요한 것은 return으로 자기 자신을 호출한다면 무한 반복이 되기 때문에
재귀함수를 작성할 때는 탈출구를 만들어줘야합니다.
여기서 탈출구는 인자가 가장 작은 수에 도달했을 때 출력되는 값을 적어주는 것입니다.
따라서 조건에 충족하면 값을 return하고, 아래 이미지와 같이 값이 출력됩니다.

그렇다면 for문, while문과 같이 반복문으로 풀면 안될까?
사실 재귀 문제들은 반복문으로도 충분히 풀 수 있다.
하지만 가끔 반복문이 복잡하게 들어가거나 무리한 메모리를 요구하는 경우들이 있다.
(예를 들어서 배열 안에 배열들을 검색할 때, for문이 2개 이내로 해결이 안될 때)
이러한 경우에 재귀함수를 활용한다면 쉽게 해결할 수 있다.
그리고 몇몇의 자료구조에서 재귀함수를 활용하는 경우가 종종 있다.
이제 하노이 탑 문제를 보도록 하겠습니다.
https://www.acmicpc.net/problem/11729
11729번: 하노이 탑 이동 순서
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로
www.acmicpc.net
1. 문제

2. 예제

3. 풀이
이 문제는 재귀함수로 문제를 해결해야 하기 때문에 입력값이 1부터 20까지라는 제한이 걸려있는 것으로 추측됩니다.
코드를 작성하기 전에 하노이 탑을 해결하는 방법에 대해서부터 알아보겠습니다.
하노이 탑에는 중요한 두가지 조건이 있습니다.
1. 한 번에 한 개의 원판만 다른 탑으로 옮길 수 있다.
2. 작은 원판 위에 큰 원판을 올려둘 수 없다.
원판의 개수가 3개일 때..

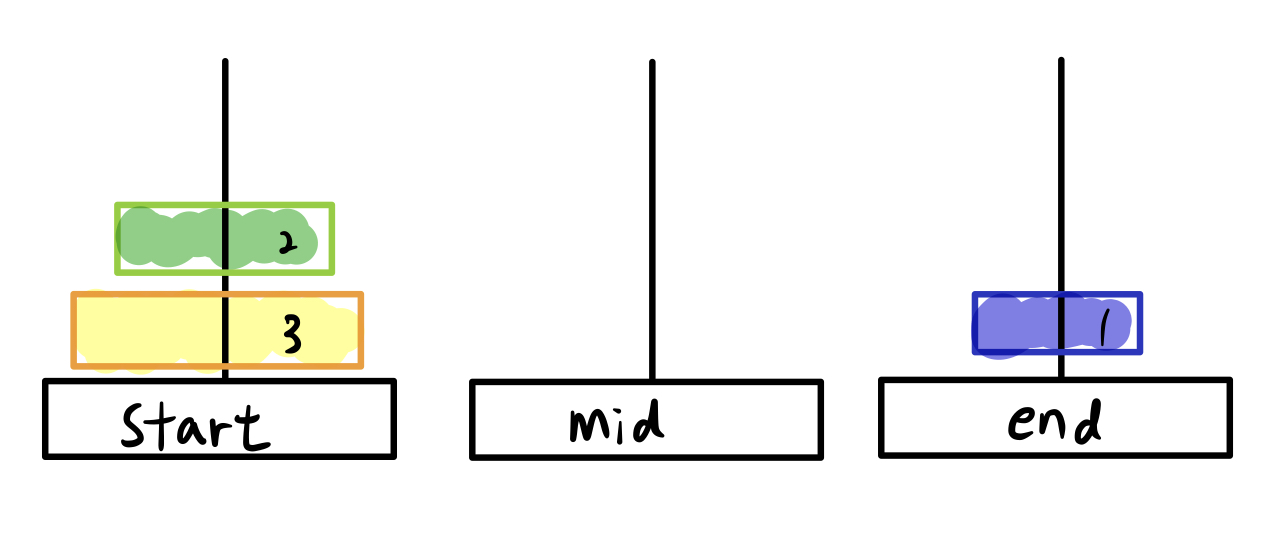


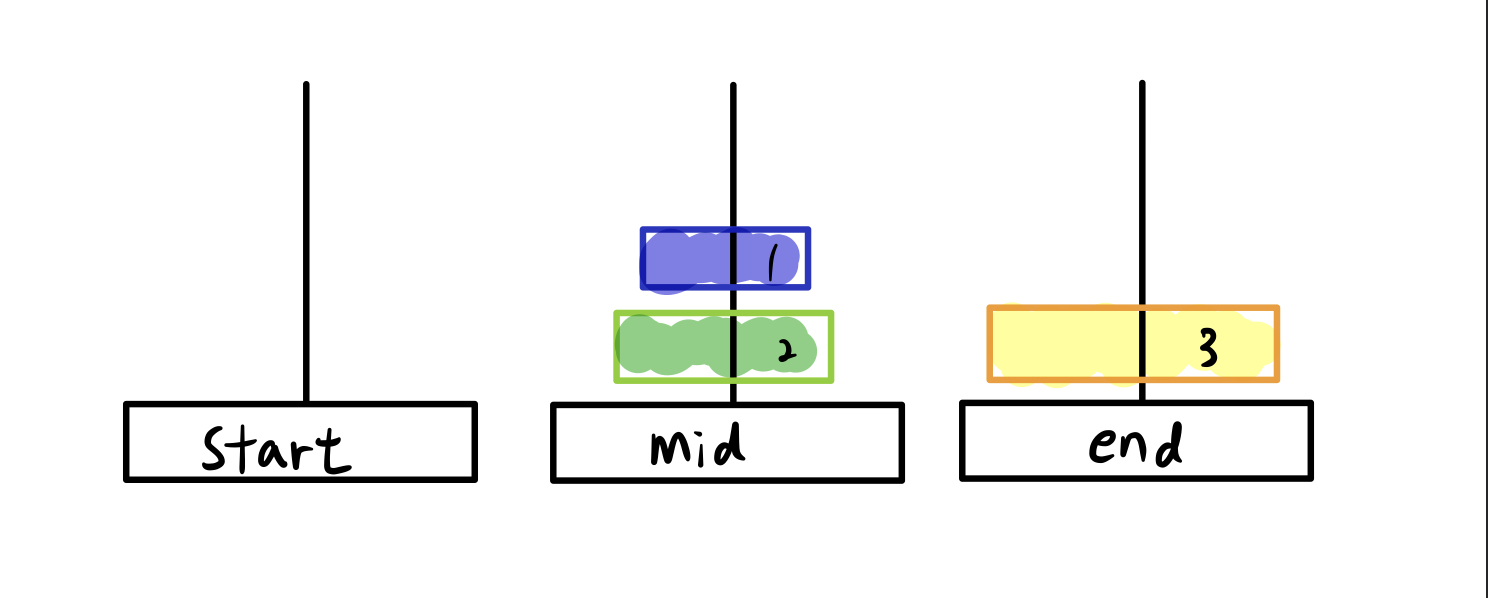



실제로 하노이 탑을 움직인다면 원판이 3개일 때는 총 7번의 움직임으로 위 같은 과정을 알 수 있습니다.
start를 1번 mid를 2번 end를 3번이라고 했을 때 가장 위 원판이 움직이는 위치를 출력한 것이 이 문제에서 원하는 결과입니다. 결과는 아래와 같이 나오면 성공입니다.
7
1 3
1 2
3 2
1 3
2 1
2 3
1 3
그렇다면 이것을 어떻게 재귀함수 알고리즘으로 해결할 수 있을까요?
원판의 개수는 3개 외에도 20개까지 있을 수 있습니다. 그렇다면 원판의 개수를 n개라고 가정하겠습니다.

각 타워의 이름은 start, mid, end라고 하겠습니다.
문제의 목표는 원판들을 start에서 end로 보내는 것입니다.
이 문제를 쉽게 이해하기 위해서는 가장 먼저 n이 1일때를 가정해봅니다.
그럼 원판은 mid를 거치지 않고 start에서 end로 이동해주면 됩니다.
만약 n이 2라면 어떨까요?
작은 원판 위에 큰 원판을 둘 수 없기 때문에 원판1을 mid로 옮긴 뒤 원판2를 end로 옮깁니다.
그 다음 원판1을 mid에서 end로 옮깁니다.
n이 3일 때는 어떨까요? 이때도 마찬가지로 원판1과 2를 규칙에 맞게 mid로 옮긴 뒤에 원판3을 end로 옮깁니다. 이어서 원판 1과 2를 end로 옮깁니다.
n이 4일 때도 똑같습니다. 이렇듯 하노이 탑에서는 가장 큰 원판(높은 수)을 end로 옮기기 위해서는 그 전까지에 원판들을 mid로 옮겨둬야 합니다.
정리하면
가장 위에 위치한 원판(원판1)을 제외한 나머지 원판들을 목적지로 옮기기 위해서는 그 전까지의 원판들을 목적지 타워가 아닌 별도의 타워에 모아둬야 합니다. 여기서 중요한 것은 별도의 타워에 모아둘 때도 하노이 탑의 규칙을 준수해야 합니다.
따라서
아래 사진과 같이 n을 3번 타워로 옮기기 위해서는 아래와 같이 1~ n-1개의 원판을 2번 타워로 옮겨야합니다.

그렇다면 1부터 n-1의 원판은 1번이 start가 되고 2번이 목적지인 end가 됩니다.
모두 옮겼다면,
이제 n의 원판을 1번에서 3번으로 옮깁니다. 여기서는 3번이 end가 됩니다.
마지막으로 1부터 n-1의 원판을 3번으로 모두 옮깁니다. 여기서는 2번 타워가 start, 3번 타워가 end입니다.
참고!
각 타워는 1번, 2번, 3번에 해당합니다.
그리고 원판이 출발하는 위치를 start
원판이 가야할 목적지는 end
임시로 보관될 장소를 mid
라고 생각하면 이해가 쉽습니다.
코드 작성
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
static StringBuilder sb = new StringBuilder();
static void move(int N, int start, int mid, int end) {
// N이 1일 때 재귀함수 종료 메소드 작성
if(N==1) {
sb.append(start + " " + end).append("\n");
return;
}
move(N-1,start,end,mid); // 1~N-1 원판까지 mid 위치로 이동하기 위한 함수
sb.append(start + " " + end).append("\n"); // N 원판을 end 위치로 옮기는 함수
move(N-1,mid,start,end); // 1~N-1 원판들을 mid 위치에서 end 위치로 옮기는 함수
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine()); // 원판의 개수 입력
//하노이 탑은 최소 [2^n -1] 번 움직임으로 모두 옮길 수 있습니다.
sb.append((int) (Math.pow(2,N)-1)).append("\n");
move(N,1,2,3);
System.out.println(sb);
}
}① 하노이 탑의 원판 이동 횟수는 2^N -1번 입니다.
Math 클래스의 pow 메소드를 활용합니다.
② 4개 인자를 파라미터로 받는 재귀 함수를 선언합니다.
move(원판의개수(N), 시작 타워(start), 임시 저장 타워(mid), 목적지 타워(end))
③ 최소 원판의 개수(1)일 때 재귀함수를 종료하도록 return을 지정해줍니다.
④ 재귀함수 활용
a. 1 ~ (N-1) 까지 원판을 모두 mid로 이동시킵니다.
b. N 원판을 start에서 end로 옮깁니다.
c. 1~(N-1) 까지 원판을 mid에서 end로 이동시킵니다.
⑤ StringBuilder를 통해서 append한 결과들을 한번에 출력합니다.
4. 결과

문제를 풀면서도, 풀이를 작성하면서도 느꼈는데
쉬운 문제가 아닌 것 같습니다.
재귀에 대해서 명확하게 좋을 것 같습니다.
* 자기 자신을 호출하는 함수
* 어느 조건에 도달했을 때 재귀를 빠저나올 수 있도록 return
'개발 > DS&Algorithms' 카테고리의 다른 글
| [자료구조] 큐(Queue)와 스택(Stack) 알아보기 (5) | 2022.03.30 |
|---|---|
| [자료구조] 배열(array) 알아보기 (6) | 2022.03.28 |
| [백준] 소인수분해_11653_자바 (4) | 2022.02.15 |
| [백준] ACM 호텔_10250_자바 (0) | 2022.02.11 |
| [백준] 알파벳 찾기_10809_자바 (6) | 2022.02.05 |



