안녕하세요😎 백엔드 개발자 제임스입니다 :)
오늘은 [깊이 우선 탐색] 이라는 문제를 포스팅하려고 합니다. 그래프와 관련된 문제를 해결할 때, 두 가지의 해결법이 있습니다. 첫 번째는 깊이 우선 탐색(Depth-First Search)이고, 두 번째는 너비 우선 탐색(Breadth-First Search)입니다. 이번 문제는 깊이 우선 탐색의 개념을 이해할 수 있도록 만들어졌습니다.
24479번 깊이 우선 탐색1 문제는 오름차순으로 인접 정점에 방문하는 방식이고, 24480번 깊이 우선 탐색2 문제는 내림차순으로 인접 정점에 방문하는 방식입니다. 따라서 두 문제를 풀이하는 방법은 크게 차이가 없습니다.
24479번 문제의 자세한 점은 아래 링크를 참고해주세요.
https://www.acmicpc.net/problem/24479
24479번: 알고리즘 수업 - 깊이 우선 탐색 1
첫째 줄에 정점의 수 N (5 ≤ N ≤ 100,000), 간선의 수 M (1 ≤ M ≤ 200,000), 시작 정점 R (1 ≤ R ≤ N)이 주어진다. 다음 M개 줄에 간선 정보 u v가 주어지며 정점 u와 정점 v의 가중치 1인 양
www.acmicpc.net
Problem
N개의 정점과 M개의 간선으로 구성된 무방향 그래프(undirected graph)가 있습니다. 정점은 1번부터 N번이고, 모든 간선의 가중치는 1입니다. 이때 임의의 정점 R 번에서 시작하여, 오름차순으로 깊이 우선 탐색을 진행하는데 방문하게 되는 정점의 순서를 출력합니다.
단, 시작 정점에서 방문할 수 없는 경우 0을 출력합니다.
풀이 아이디어
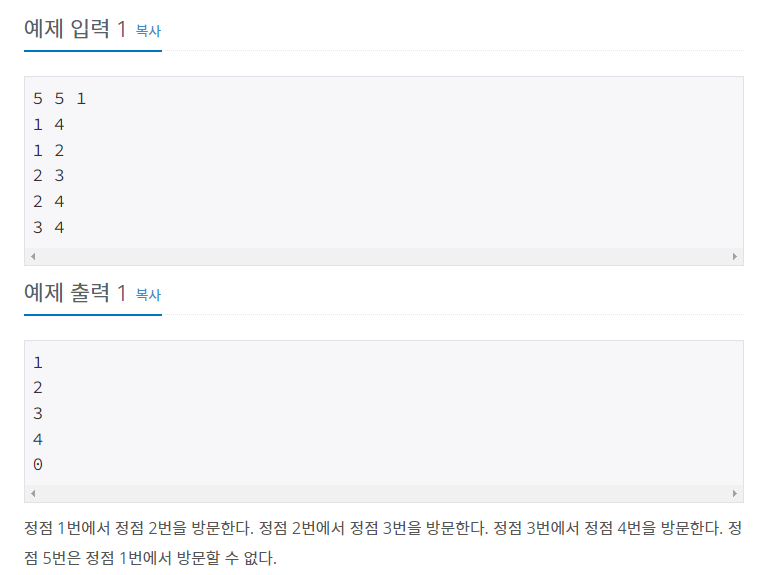
먼저 문제의 예제 입력을 보도록 하겠습니다.

가장 첫 줄은 각각 정점의 수(N), 간선의 수(M), 시작 정점(R)을 나타냅니다. 즉, 5개의 정점과 5개의 간선을 가진 그래프에서 1번 정점으로 탐색을 시작한다는 의미입니다. 다음 줄부터는 임의의 정점에서 어떤 정점으로 방문할 수 있는지를 나타냅니다. 가령 1과 4는 정점 1번에서 정점 4번으로 방문한다는 의미입니다. 동시에 무방향 그래프이기 때문에, 4번 정점에서 1번 정점으로 이동할 수 있다는 것도 알 수 있습니다. 이를 토대로 그래프의 형태를 정리하면 아래와 같습니다.
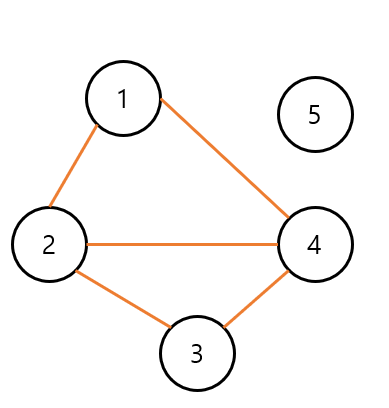
보다시피 5개의 간선을 가지나, 5번 정점은 어떤 정점과도 연결되어 있지 않습니다. 이어서 정점 1부터 시작했을 때의 각 정점의 방문 순서를 찾아보도록 하겠습니다. 이때 오름차순으로 방문해야 한다는 규칙을 잊어서는 안 됩니다.
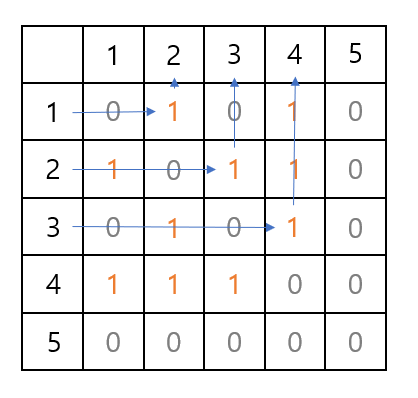
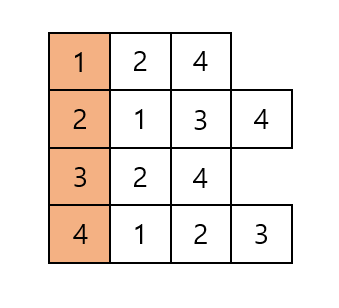
위 그림은 그래프를 2차원 테이블로 나타낸 것입니다. 열과 행은 정점을 나타냅니다. 내부에 적힌 정보는 방문 여부입니다.
(1) 정점 1번은 정점 2번과 정점 4번으로 이동할 수 있습니다. 오름차순 정렬이기 때문에 먼저 2번으로 이동합니다.
(2) 정점 2번은 정점 1번, 3번, 4번으로 이동할 수 있습니다. 1번은 이미 방문을 했기 때문에 다음 3번으로 이동합니다.
(3) 정점 3번은 정점 2번, 4번으로 갈 수 있습니다. 역시나 2번을 방문했기 때문에 4번으로 이동합니다.
(4) 정점 5번이 어떤 정점과도 연결되지 않았기 때문에, 정점 4번을 방문했을 때 프로세스가 종료됩니다.
위 과정을 거친다면, 아래와 같이 될 것입니다.
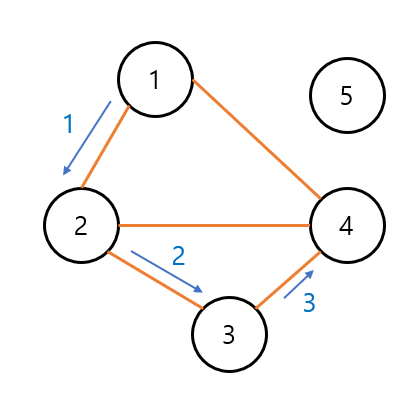
이제 방문 순서를 보겠습니다. 가장 먼저 시작 정점도 방문 정점으로 포함시키기 때문에, 정점 1번이 첫 번째 방문입니다. 이어서 정점 2번, 정점 3번, 정점 4번 순으로 방문하고 정점 5번은 방문하지 않기 때문에 결과는 [1, 2, 3, 4, 0] 이 됩니다.
이와 같이 깊이 우선 탐색은 root 노드의 자식 노드들을 우선적으로 탐색하기 때문에 재귀를 활용해서 문제를 해결할 수 있습니다. 단, 우리가 체크해야 할 것은 '방문했던 정점'인가입니다.
이제 코드 작성을 통해서 문제를 해결하도록 하겠습니다.
코드를 작성하기 전에! (Error)
코드를 작성하기 전에 주의해야 할 점이 있습니다. 풀이 아이디어에서 언급했던 테이블 형태로 구현하면 메모리 초과 문제가 발생합니다. 즉, 이차원 배열로 그래프를 구현하면 안 됩니다. 저 또한 이중배열을 통해 문제는 해결했으나, 백준에 제출했을 땐 '메모리 초과'라는 결과를 맞이하게 되었습니다.


따라서 이차원 배열 대신 이중 List의 형태로 graph를 형성하면 메모리를 절약할 수 있습니다. List 형태로 만든 그래프는 아래와 같습니다.
이 문제에서 HashMap<Integer,ArrayList<Integer>>, Queue<Integer>, ArrayList<ArrayList<Integer>>, PriorityQueue<Integer>를 활용한다면 좀 더 효율적으로 구현할 수 있습니다.
코드 작성
(1) 이중 ArrayList로 graph를 구현했습니다.
(2) 방문하는 정점은 또 다른 배열에 저장했습니다.
(3) 그래프를 순회할 때, 배열에 저장되었는지를 체크하며 방문 여부를 파악했습니다.
(4) 순회를 마치면 저장된 배열에서 값을 꺼내며, 순서를 매깁니다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
// 1076ms
// 오름차순
public class Main {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static StringTokenizer st;
static StringBuilder sb = new StringBuilder();
static ArrayList<ArrayList<Integer>> graph = new ArrayList<>(); // 정점들의 정보를 기록할 그래프
static int[] check; // 방문한 정점을 기록할 배열
static int count; // 방문 순서
public static void main(String[] args) throws IOException {
st = new StringTokenizer(br.readLine());
int vertex = Integer.parseInt(st.nextToken());
int edge = Integer.parseInt(st.nextToken());
int startVertex = Integer.parseInt(st.nextToken());
// 방문한 정점이 최대 정점의 개수만큼 있기 때문에, 정점의 개수만큼의 크기로 배열 생성
// index 혼란을 방지하고자 0번 인덱스를 더미 데이터로 활용
check = new int[vertex+1];
// graph의 index를 정점의 개수만큼 만들어줌
for(int i =0; i < vertex+1; i++) {
graph.add(new ArrayList<>());
}
for(int i = 0; i < edge; i++) {
st = new StringTokenizer(br.readLine());
int fromVertex = Integer.parseInt(st.nextToken());
int toVertex = Integer.parseInt(st.nextToken());
// 무방향이기 때문에 양쪽으로 정보를 추가
graph.get(fromVertex).add(toVertex);
graph.get(toVertex).add(fromVertex);
}
// 오름차순을 위해 정렬
for(int i = 1; i < graph.size(); i++) {
Collections.sort(graph.get(i));
}
// 시작 정점도 순서에 포함이므로 count 초기값 1 할당
count = 1;
// 깊이 우선 탐색 재귀 시작
dfs(startVertex);
// 각 인덱스별로 방문 순서가 기록된 배열을 순회하며, 값을 StringBuilder에 저장
for(int i = 1; i < check.length; i++) {
sb.append(check[i]).append("\n");
}
System.out.println(sb);
}
// 깊이 우선 탐색 메서드
private static void dfs(int vertex) {
check[vertex] = count; // 현재 방문하고있는 정점에 순서 저장
// 현재 위치한 정점이 갈 수 있는 정점 리스트를 순회
for(int i = 0; i < graph.get(vertex).size(); i++) {
int newVertex = graph.get(vertex).get(i);
//다음 갈 정점을 방문했었는지 체크(0일 경우 방문 X)
if(check[newVertex] == 0){
count++;
dfs(newVertex);
}
}
}
}코드에 주석을 추가하니 많이 길어졌네요. 위 내용을 요약하자면 아래와 같습니다.
1) 정점이 1부터 시작하므로 인덱스와 혼란이 올 수 있습니다. 따라서 저는 배열의 크기를 지정할 때 +1을 시켜서, 인덱스 0번에 더미 데이터를 만들어 주었습니다.
2) 무방향 그래프이기 때문에, 현재 정점에서 다음 방문할 정점의 정보를 추가하고, 방문한 정점에서도 현재 정점의 정보를 똑같이 추가합니다. 즉, 양쪽으로 정보를 추가해주는 것입니다.
3) 오름차순으로 탐색하기 위해 각각의 정점들이 갖는 리스트들을 Collections.sort() 메서드로 정렬했습니다. 따라서 오름차순 조건을 만족시킬 수 있었습니다. 만약 내림차순으로 탐색하고 싶다면, 반대로 내림차순으로 정렬해주면 됩니다.
4) 다음 방문할 정점이 이전에 방문했었는지 꼭 체크해야 합니다. 만약 체크하지 않는다면, 무한 루프에 빠지게 됩니다.
'개발 > DS&Algorithms' 카테고리의 다른 글
| [프로그래머스/JAVA] Level 2, 다리를 지나는 트럭 (2) | 2022.11.11 |
|---|---|
| [프로그래머스/JAVA] Level 1, 완주하지 못한 선수 (42576) (2) | 2022.10.17 |
| [백준] 포도주 시식_2156_자바 (5) | 2022.08.10 |
| [백준] 프린터 큐_1966_자바 (2) | 2022.07.29 |
| [백준] 평범한 배낭 (DP)_12865_자바 (4) | 2022.07.03 |



