안녕하세요 이번 게시글에서는 자료 구조 트리(Tree)에 대해서 알아보도록 하겠습니다.
트리(Tree)
트리(Tree)란, 노드들이 나무 가지처럼 연결된 비선형 계층형 자료구조입니다. 아래 그림과 같이 트리 자료구조는 나무를 뒤집은 모양과 유사합니다. 따라서 가장 위에 있는 노드를 Root(뿌리) 노드라고 합니다. 이러한 트리는 탐색(검색) 알고리즘 구현을 위해 많이 사용됩니다.


01. 트리의 종류

02. 알아둘 용어
- Node : 트리에서 데이터를 저장하는 기본 요소
(노드에는 다른 연결된 노드에 대한 Branch 정보가 포함) - Branch : 간선(edge)라고도 하며, 노드와 노드를 연결하는 선
- Root Node : 트리에서 가장 위에 있는 노드
- Level : 최상위 노드를 Level 0이라고 했을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
- Parent Node : 어떤 노드의 상위 레벨에 연결된 노드
- Child Node : 어떤 노드의 하위 레벨에 연결된 노드
- Leaf Node (Terminal Node) : Child Node 가 하나도 없는 노드
- Sibling (Brother Node) : 동일한 Parent Node를 가진 노드
- Depth : 트리에서 Node 가 가질 수 있는 최대 Level
03. 트리의 특징
- 트리는 그래프의 한 종류로, '최소 연결 트리'라고도 불림
- 트리는 계층 모델로 이루어짐
- DAG(Directed Acyclic Graphs, 방향성이 있는 비순환 그래프의 한 종류
- 사이클이 없음 - 노드가 N개인 트리는 항상 N-1개의 간선(edge)을 가짐
- 트리는 이진 트리, 이진 탐색 트리, 균형 트리(AVL 트리, red-black 트리), 이진 힙(최대 힙, 최소 힙) 등이 있음
* 이진 트리와 이진 탐색 트리(Binary Search Tree)
- 이진 트리 : 노드의 최대 브랜치가 2인 트리
- 이진 탐색 트리(Binary Search Tree, BST) : 이진 트리에 추가 조건이 있음
ex) 왼쪽 노드는 해당 노드보다 작은 값, 오른쪽 노드는 해당 노드보다 큰 값을 가짐.
04. 이진 탐색 트리 (Binary Search Tree) 코드 작성
이진 탐색 트리를 코드로 구현하기 위해서는 먼저 다양한 CASE를 분석해야 합니다.
기능을 구현하기 전에 자료구조에서 사용할 노드는 아래와 같이 코드를 작성했습니다.
/**
* 노드
*/
public class Node {
int value; // 노드가 갖는 data
Node left; // 왼쪽 노드
Node right; // 오른쪽 노드
// 노드를 처음 생성할 때
public Node(int value) {
this.value = value;
this.right = null;
this.left = null;
}
}
1) 구현할 기능
- 노드 추가 기능
- 노드 검색 기능
- 노드 삭제 기능
2) CASE 분석
#1 노드 추가 기능
CASE 1 : 노드가 하나도 없을 때 (Root 노드가 null 일 때)
해당 경우에는 root(head) 노드에 새로운 노드를 생성하면 됩니다.
* root node를 임의로 head라고 하겠습니다.
insertNode(14);

CASE 2 : 노드가 하나 이상 있을 때
이 경우에는 순회를 하면서 추가하는 데이터가 비교 노드의 데이터보다 작을 경우에는 왼쪽, 보다 클 경우에는 오른쪽으로 이동하면서 null을 찾고 해당 데이터의 노드를 생성하면 됩니다.
예를 들어서 HEAD에 14 라는 수가 있을 때 8을 추가하면 아래와 같이 됩니다.

만약 아래와 같이 이미 노드들이 있다고 생각해봅시다. 여기서 새로운 데이터로 6을 추가한다면 어떻게 될까요?

먼저 HEAD와 비교합니다. (1) 6은 14보다 작기 때문에 왼쪽 노드로 이동하게 됩니다. 이처럼 노드를 비교하면서 null 을 찾는 것인데요. 다음 노드는 null이 아닌 8이기 때문에 또 비교를 합니다. 이번도 역시 (2) 6은 8보다 작기 때문에 왼쪽 노드로 이동합니다. 다음은 4와 비교를 진행합니다. 여기서는 (3) 6이 4보다 크기 때문에 오른쪽 노드로 이동합니다. 하지만 4의 오른쪽 노드는 null입니다. 그래서 6은 4의 오른쪽 노드에 생성되게 됩니다. 아래 그림과 같게 되는 것이죠.

이 같은 방법으로 CASE를 다시 정리하자면,
CASE 2-1 : 추가하는 데이터가 비교 데이터보다 작을 경우
CASE 2-2 : 추가하는 데이터가 비교 데이터보다 크거나 같을 경우
코드는 아래와 같이 작성할 수 있습니다.
/**
* 노드 추가 기능
*
* @param 노드의 value
* @return true / false
*/
public boolean insertNode(int data) {
// CASE 1 : 노드가 한 개도 없을 때
if (this.head == null) {
this.head = new Node(data);
// CASE 2 : 노드가 한개 이상 있을 때
} else {
// 비교할 노드
Node currNode = this.head;
while (true) {
// CASE 2-1 : 추가하는 데이터가 비교 데이터보다 작을 때
if (data < currNode.value) {
// null 이 아닐 경우, 비교 노드의 왼쪽 노드로 이동한 후 다시 비교한다.
if (currNode.left != null) {
currNode = currNode.left;
// 비교 노드의 왼쪽이 null 일 경우
} else {
currNode.left = new Node(data);
break; // while 을 종료한다.
}
// CASE 2-2 : 추가하는 데이터가 비교 데이터보다 크거나 같을 때
} else {
// null 이 아닐 경우, 비교 노드의 오른쪽 노드로 이동한 후 다시 비교한다.
if (currNode.right != null) {
currNode = currNode.right;
// 비교 노드의 오른쪽이 null 일 경우
} else {
currNode.right = new Node(data);
break; // while 을 종료한다.
}
}
}
}
return true; // 새로운 노드가 추가되었으므로 true를 반환
}#2 노드 검색 기능
노드 검색 기능은 특별한 CASE가 있지 않아서 비교적 간단한 편입니다.
검색은 HEAD로부터 시작해서 전체를 순회하고 원하는 데이터가 있을 때 해당 노드를 반환하면 됩니다. 만약 전체를 순회했음에도 데이터가 없다면, null을 반환하겠죠? 또한 애초에 Node가 없어도 nulll을 반환하게 됩니다.
데이터를 추가할 때와 같이 찾을 때도 비교 데이터보다 작을 경우와 클 경우로 생각해서 왼쪽/ 오른쪽으로 이동하면 됩니다.

여기서 4를 찾는다고 했을 때 먼저 14와 비교합니다. 4는 14보다 작으니 왼쪽 노드로 이동합니다. 이어서 8과 비교하는데 역시나 4는 8보다 작으니 8 노드의 왼쪽 노드로 이동합니다. 그럼 4를 발견합니다. 순회를 종료하고, 4의 노드를 반환하면 됩니다.
이 같은 방법으로 원하는 노드를 찾기 때문에 다른 검색 방법에 비해 빠르고 효율적으로 검색할 수 있습니다.
코드로 작성하면 아래와 같습니다.
/**
* 노드 검색하기
*
* @param 찾으려는 노드의 데이터
* @return 해당 데이터 반환
*/
public Node search(int data) {
// 비교 노드
Node currNode = this.head;
// 비교 노드가 null이 아닐 때 순회합니다.
// currNode가 null일 때, while은 종료가 됩니다.
while (currNode != null) {
// 찾는 데이터가 비교 노드의 값일 때 해당 노드를 반환
if (data == currNode.value) {
return currNode;
// 비교 노드의 값이 찾는 데이터가 아닐 때
} else {
// 찾는 데이터가 비교 노드의 값보다 작을 때
if(data < currNode.value) {
// 비교 노드는 현재 비교 노드의 왼쪽 자식 노드로 이동
currNode = currNode.left;
// 찾는 데이터가 비교 노드의 값보다 클 때
} else {
// 비교 노드는 현재 비교 노드의 오른쪽 자식 노드로 이동
currNode = currNode.right;
}
// 조건문에 따라 비교 노드가 이동하게 됩니다.
// 이 때 데이터를 찾거나, 비교 노드가 null이 되는 상황까지 순회를 하게 되는 것입니다.
}
}
// 만약 비교 노드가 null 이여서 while문이 종료된 것이라면, 찾는 노드가 없다고 null을 반환해줍니다.
return null;
}
#3 노드 삭제 기능
노드 삭제 기능에 경우는 정말 다양한 CASE 가 존재합니다. 따라서 코드가 상당히 복잡하여 포스팅에서 전부 다룰 수 없게 되었습니다. 때문에 해당 기능의 자세한 코드는 Github을 참고해주세요.
https://github.com/Si-Hyeak-KANG/java_algorithm/blob/master/src/dataStructureSudy/base01/MyBST.java
GitHub - Si-Hyeak-KANG/java_algorithm: JAVA를 활용한 코딩 테스트 공부
JAVA를 활용한 코딩 테스트 공부 . Contribute to Si-Hyeak-KANG/java_algorithm development by creating an account on GitHub.
github.com
먼저 가볍게 트리에 HEAD 노드 한 개만 있다고 생각하겠습니다. 만약 삭제할 노드가 HEAD 데이터이고, 연결된 노드가 없다면 그냥 삭제하면 되겠죠?

하지만 왼쪽이든 오른쪽이든 한 개라도 연결되었으면 어떻게 되었을까요?


HEAD가 삭제되었기 때문에 1번은 8이 HEAD가 되고, 2번은 18이 HEAD가 됩니다.
그렇다면 HEAD에 왼쪽 오른쪽 둘 다 연결되어 있으면 어떻게 될까요?
이때는 노드를 삭제하고, 삭제한 노드의 오른쪽 자식 노드 중에서 가장 작은 값의 노드로 삭제한 노드의 자리를 대체합니다. 아래와 같이 되는 것입니다.


위 이미지를 보면 16 노드가 HEAD로 이동하고 18 노드의 왼쪽 자식 노드가 없어지는 것을 알 수 있습니다. 여기서 또 고려해봐야 하는 것은 만약 16 노드의 자식 노드가 있었다면 어땠을까요?

만약 16 노드의 자식 노드가 있었다고 가정하겠습니다. 여기서 중요한 것은 16 노드의 왼쪽 자식 노드는 있을 수는 없습니다. 만약 왼쪽 자식 노드가 있었다면, HEAD에는 15가 대체되어야 합니다. 따라서 우리는 왼쪽 자식 노드는 없다고 생각해야 합니다.
다시 돌아와서 16 노드가 HEAD로 이동한다면, 16 노드의 오른쪽 자식 노드인 17이 18 노드의 왼쪽 자식 이 되는 것입니다. 최종적으로는 아래 그림과 같이 되는 것이죠.
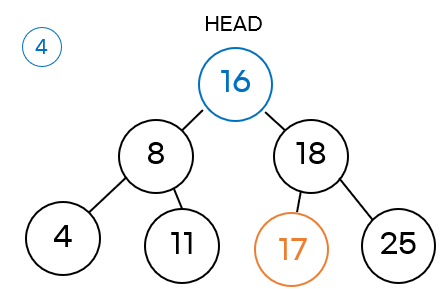
이제 이렇게 복잡한 내용을 CASE 별로 정리해보도록 하겠습니다.
CASE 1 : 삭제할 노드가 Leaf 노드일 경우 ( 자식 노드가 하나도 없을 경우)


위 그림은 자식 노드가 없는 Leaf 노드인 16 노드를 삭제하는 경우입니다. 이처럼 Leaf 노드를 삭제할 때는 어떠한 노드로 대체할 필요도 없고, 부모 노드의 자식 노드도 null이 됩니다.
CASE 2 : 삭제할 노드가 왼쪽 자식 노드만 갖고 있을 경우


위 그림은 왼쪽 자식 노드만 갖고 있는 8 노드를 삭제하는 경우입니다. 이때 14의 왼쪽 자식 노드는 4가 됩니다.
CASE 3 : 삭제할 노드가 오른쪽 자식 노드만 갖고 있을 경우


위 그림은 오른쪽 자식 노드만 갖고 있는 8 노드를 삭제하는 경우입니다. 이 때 14의 왼쪽 자식 노드는 11이 됩니다.
CASE 4 : 삭제할 노드가 왼쪽, 오른쪽 자식 둘 다 갖고 있을 경우
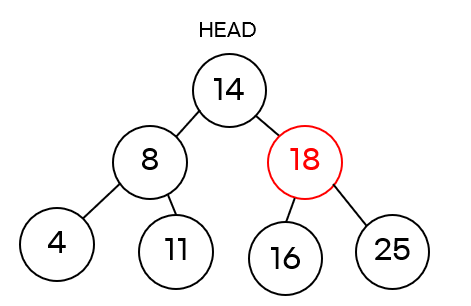

위 그림은 두 개자식 노드를 가진 18 노드를 삭제하는 경우입니다.
이 때는 18 노드의 오른쪽 자식 노드에서 가장 작은 수 25 노드가 18을 대체하게 됩니다. 따라서 14 노드의 오른쪽 자식 노드는 25 노드가 되고 18을 대체했기 때문에 25 노드는 왼쪽 자식 노드로 16 노드를 갖게 됩니다.
만약 25 노드에도 아래 그림과 같이 자식 노드를 갖고 있었다고 가정한다면,


24 노드가 18 노드의 자리로 들어가고, 14 노드의 오른쪽 자식 노드로 24 노드가 되고 18 노드의 자식 노드였던 16과 25는 24 노드와 연결되게 됩니다.
05. 시간 복잡도 (탐색 시)
트리의 높이(depth)를 h라고 표기하고, n 개의 노드를 갖는다면
h =log₂n 에 가깝습니다. 따라서 시간 복잡도는 O(logn)이 됩니다. 실제로 비교 노드보다 작은지 큰지에 따라 왼쪽 오른쪽으로 나눠지기 때문에 진행할 때마다 50% 씩 시간이 단축됩니다.
참고 : 빅오 표기법에서 log의 밑은 10이 아니라 2입니다.
하지만 이것은 트리가 제대로 만들어졌을 때 상황입니다.
만약 root 노드가 1이고 이후 추가하는 노드가 2, 3, 4, 5처럼 점점 커진다면, 아래 그림과 같이 직선의 형태를 나타낼 것입니다.

이 경우는 최악의 상황으로 링크드 리스트, 배열 등과 동일한 성능인 시간 복잡도 O(n)이 발생하게 됩니다.
다음 포스팅에서는 트리와 유사한 힙(Heap) 자료구조에 대해서 알아보도록 하겠습니다.
'개발 > DS&Algorithms' 카테고리의 다른 글
| [알고리즘] 버블 정렬(bubble sort) 알아보기 (16) | 2022.04.21 |
|---|---|
| [자료구조] 힙(Heap) 알아보기 (10) | 2022.04.14 |
| [자료구조] 해시(HASH) 알아보기 (2) | 2022.04.07 |
| [자료구조] 연결 리스트(Linked List) 알아보기 (6) | 2022.04.01 |
| [자료구조] 큐(Queue)와 스택(Stack) 알아보기 (5) | 2022.03.30 |



